Trong lĩnh vực phân tích dữ liệu và học máy, hồi quy logistic (Logistic Regression) là một công cụ quan trọng giúp dự đoán kết quả của các biến phân loại. Với khả năng ứng dụng rộng rãi, từ tài chính, y tế đến tiếp thị, mô hình này giúp các tổ chức khai thác dữ liệu hiệu quả, đưa ra quyết định chính xác. Bài viết này sẽ giúp bạn hiểu rõ hơn về Logistic Regression là gì? Cách hoạt động, thuật ngữ quan trọng và những ứng dụng thực tế. Đọc ngay!
Logistic Regression là gì?
Hồi quy logistic (Logistic Regression) là một phương pháp phân tích dữ liệu sử dụng các phép toán để xác định mối quan hệ giữa các biến số (yếu tố dữ liệu). Dựa trên mối quan hệ đã tìm thấy, kỹ thuật này có thể dự đoán giá trị của một biến số dựa trên (các) biến số còn lại. Kết quả dự đoán thường là một giá trị rời rạc (discrete value), ví dụ: “Có” hoặc “Không”, “True” hoặc “False”.
Ví dụ minh họa, bạn muốn dự đoán liệu khách truy cập website có nhấp vào nút “Thanh toán” trong giỏ hàng hay không. Phân tích hồi quy logistic sẽ xem xét các hành vi trong quá khứ của khách hàng, như thời gian họ ở trên trang, số lượng sản phẩm trong giỏ.
Từ đó xác định rằng, nếu khách truy cập ở lại trang trên 5 phút và thêm hơn 3 sản phẩm, khả năng cao họ sẽ nhấp “Thanh toán”. Dựa vào đó, mô hình hồi quy logistic có thể dự đoán hành vi của khách hàng mới.
Tại sao hồi quy Logistic lại quan trọng?
Hồi quy logistic là một kỹ thuật nền tảng trong lĩnh vực trí tuệ nhân tạo (AI) và học máy (ML). Các mô hình ML, về bản chất là các chương trình phần mềm, có thể được huấn luyện để thực hiện các tác vụ xử lý dữ liệu phức tạp mà không cần sự can thiệp trực tiếp của con người.
Mô hình ML dựa trên hồi quy logistic giúp các tổ chức khai thác thông tin chi tiết (insights) từ dữ liệu kinh doanh. Các tổ chức có thể sử dụng những thông tin chi tiết này cho phân tích dự đoán (predictive analysis), giúp giảm chi phí hoạt động, nâng cao hiệu quả, và mở rộng quy mô nhanh chóng.
Ví dụ, một công ty có thể phát hiện ra các yếu tố giúp giữ chân nhân viên, hoặc thiết kế các sản phẩm có khả năng sinh lời cao hơn. Tối ưu hóa hoạt động là một điểm mạnh.
Dưới đây là một số lợi ích khi so sánh hồi quy logistic với các kỹ thuật ML khác:
- Đơn giản: Các mô hình hồi quy logistic có độ phức tạp toán học thấp hơn so với các phương pháp ML khác. Điều này cho phép triển khai chúng ngay cả khi đội ngũ của bạn không có chuyên môn sâu về ML. Dễ tiếp cận.
- Tốc độ: Mô hình hồi quy logistic có thể xử lý khối lượng lớn dữ liệu với tốc độ cao, do yêu cầu về tài nguyên tính toán (bộ nhớ, sức mạnh xử lý) thấp hơn. Điều này khiến chúng trở nên lý tưởng cho các tổ chức mới bắt đầu với các dự án ML, mong muốn đạt được kết quả nhanh chóng.
- Linh hoạt: Hồi quy logistic có thể giải quyết các bài toán có hai hoặc nhiều kết quả đầu ra rời rạc. Nó cũng có thể được sử dụng để tiền xử lý dữ liệu. Ví dụ, bạn có thể phân loại dữ liệu có phạm vi giá trị lớn (ví dụ: giao dịch ngân hàng) thành phạm vi nhỏ hơn bằng hồi quy logistic. Sau đó, tập dữ liệu đã được xử lý này có thể được phân tích bằng các kỹ thuật ML khác để tăng độ chính xác.
- Tính minh bạch (Interpretability): Phân tích hồi quy logistic cho phép các nhà phát triển hiểu rõ hơn về các quy trình phần mềm bên trong so với các kỹ thuật phân tích dữ liệu khác. Việc gỡ lỗi và sửa lỗi cũng trở nên dễ dàng hơn do các phép toán ít phức tạp.
Cách hoạt động của Logistic Regression
Để hiểu rõ cách thức hoạt động của mô hình hồi quy logistic, chúng ta cần xem xét các khái niệm về phương trình và biến số.
Phương trình (Equation)
Trong toán học, một phương trình biểu diễn mối quan hệ giữa hai biến, thường được ký hiệu là x và y. Bạn có thể sử dụng các phương trình (hay hàm số) này để vẽ đồ thị trên hệ trục tọa độ x-y bằng cách thay thế các giá trị khác nhau của x và y.
Ví dụ, xét hàm số y = 2*x. Khi vẽ đồ thị của hàm số này, ta sẽ thu được một đường thẳng. Do đó, hàm số này còn được gọi là hàm tuyến tính (linear function).
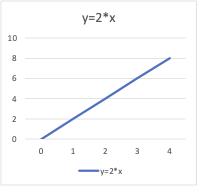
Biến số (Variables)
Trong thống kê, biến số là các yếu tố dữ liệu hoặc thuộc tính có thể nhận các giá trị khác nhau. Trong một phân tích, có những biến được coi là biến độc lập (independent variable) hay biến giải thích (explanatory variable). Đây là những yếu tố được cho là nguyên nhân gây ra sự thay đổi của một kết quả nào đó. Các biến khác được gọi là biến phụ thuộc (dependent variable) hay biến phản hồi (response variable); giá trị của chúng phụ thuộc vào giá trị của các biến độc lập.
Nói chung, hồi quy logistic nghiên cứu cách các biến độc lập ảnh hưởng đến một biến phụ thuộc bằng cách xem xét dữ liệu lịch sử của cả hai loại biến.
Trong ví dụ y = 2*x, x được gọi là biến độc lập, biến dự đoán, hoặc biến giải thích vì nó có một giá trị đã biết trước. y được gọi là biến phụ thuộc, biến kết quả, hoặc biến phản hồi vì giá trị của nó chưa biết.
Hàm hồi quy Logistic (Logistic Regression Function)
Hồi quy logistic là một mô hình thống kê sử dụng hàm logistic, còn được gọi là hàm logit, làm phương trình biểu diễn mối quan hệ giữa x và y. Hàm logit ánh xạ y như một hàm sigmoid của x.
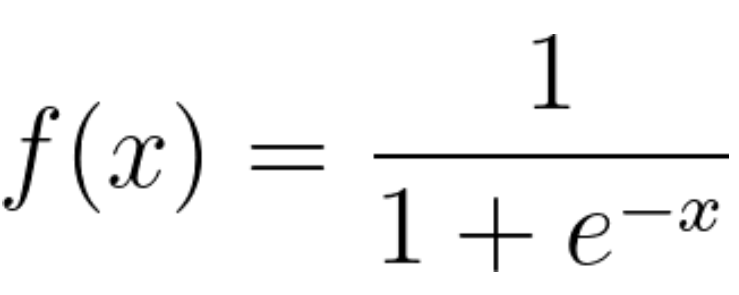
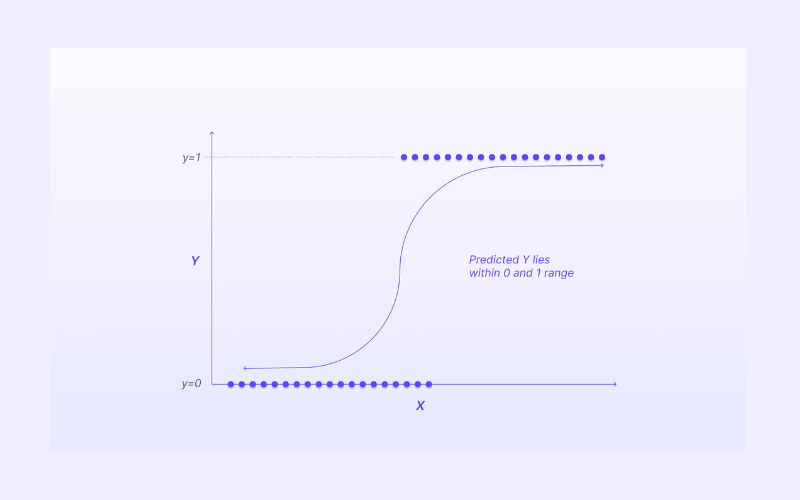
Đồ thị của phương trình hồi quy logistic có dạng đường cong chữ S (sigmoid curve).
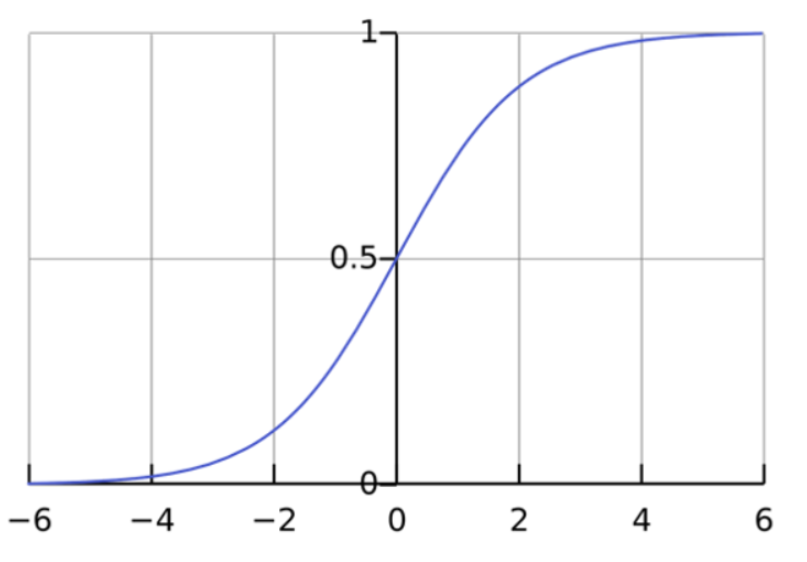
Điểm quan trọng là hàm logit luôn trả về giá trị nằm giữa 0 và 1 cho biến phụ thuộc, bất kể giá trị của biến độc lập là bao nhiêu. Đây chính là cách hồi quy logistic ước tính giá trị của biến phụ thuộc. Phương pháp hồi quy logistic cũng có thể mô hình hóa phương trình giữa nhiều biến độc lập và một biến phụ thuộc.
Phân tích hồi quy Logistic với nhiều biến độc lập
Trong nhiều trường hợp thực tế, giá trị của biến phụ thuộc bị ảnh hưởng bởi nhiều biến độc lập. Để mô hình hóa các tập dữ liệu như vậy, công thức hồi quy logistic giả định một mối quan hệ tuyến tính giữa các biến độc lập khác nhau.
Biến đầu ra cuối cùng (y) có thể được tính toán như sau:
y = f(β₀ + β₁x₁ + β₂x₂ + … + βₙxₙ)
Trong đó, ký hiệu β đại diện cho các hệ số hồi quy (regression coefficients). Mô hình logit có thể ước tính các giá trị hệ số này khi được cung cấp một tập dữ liệu đủ lớn với các giá trị đã biết của cả biến phụ thuộc và biến độc lập.
Log của tỷ số Odds (Log-Odds)
Mô hình logit cũng có thể được biểu diễn qua tỷ số thành công trên thất bại (odds ratio), hay log của tỷ số odds.
Ví dụ, nếu bạn chơi poker và thắng 4 ván trong tổng số 10 ván, tỷ số thắng của bạn là 4/6 (4 thắng, 6 thua). Đây chính là tỷ số thành công trên thất bại. Xác suất thắng của bạn là 4/10.
Về mặt toán học, tỷ số odds là p/(1 – p), trong đó p là xác suất thành công. Log của tỷ số odds là log(p/(1 – p)). Hàm logistic có thể được biểu diễn bằng log của tỷ số odds.
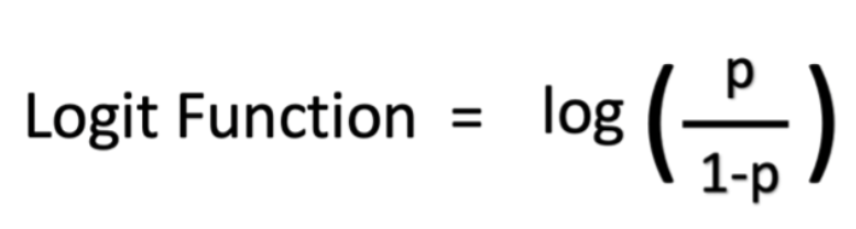
Các thuật ngữ quan trọng trong Logistic Regression
Dưới đây là một số thuật ngữ phổ biến liên quan đến hồi quy logistic:
- Biến độc lập (Independent variables): Là các yếu tố đầu vào hoặc các biến dự báo được sử dụng để đưa ra dự đoán về biến phụ thuộc.
- Biến phụ thuộc (Dependent variable): Là biến mục tiêu trong mô hình hồi quy logistic, tức là biến cần dự đoán.
- Hàm logistic (Logistic function): Công thức thể hiện mối quan hệ giữa biến độc lập và biến phụ thuộc. Hàm logistic giúp chuyển đổi biến đầu vào thành một giá trị xác suất từ 0 đến 1, thể hiện khả năng biến phụ thuộc có giá trị 1 hoặc 0.
- Tỷ lệ chấp nhận (Odds): Là tỷ lệ giữa khả năng xảy ra và không xảy ra của một sự kiện. Khác với xác suất (probability), tỷ lệ chấp nhận là tỷ lệ giữa số lần xảy ra sự kiện so với tất cả các khả năng có thể xảy ra.
- Log-odds (Hàm logit): Là logarit tự nhiên của tỷ lệ chấp nhận. Trong hồi quy logistic, log-odds của biến phụ thuộc được mô hình hóa như một tổ hợp tuyến tính của các biến độc lập và hệ số chặn.
- Hệ số hồi quy (Coefficient): Các tham số ước lượng của mô hình hồi quy logistic, thể hiện mức độ ảnh hưởng của biến độc lập lên biến phụ thuộc.
- Hệ số chặn (Intercept): Là một hằng số trong mô hình hồi quy logistic, đại diện cho log-odds khi tất cả các biến độc lập bằng 0.
- Ước lượng hợp lý tối đa (Maximum likelihood estimation – MLE): Là phương pháp được sử dụng để ước lượng các hệ số của mô hình hồi quy logistic, nhằm tối đa hóa xác suất quan sát dữ liệu theo mô hình.
So sánh giữa hồi quy tuyến tính và hồi quy logistic
Cả hồi quy tuyến tính và hồi quy logistic đều là những mô hình phổ biến trong lĩnh vực khoa học dữ liệu. Nhờ các công cụ mã nguồn mở như Python và R, quá trình tính toán cho hai mô hình này trở nên nhanh chóng và dễ dàng.
Hồi quy tuyến tính được sử dụng để xác định mối quan hệ giữa một biến phụ thuộc liên tục và một hoặc nhiều biến độc lập. Khi chỉ có một biến độc lập và một biến phụ thuộc, mô hình này được gọi là hồi quy tuyến tính đơn giản.
Khi số lượng biến độc lập tăng lên, nó được gọi là hồi quy tuyến tính bội. Với mỗi loại hồi quy tuyến tính, mục tiêu chính là vẽ một đường phù hợp nhất với tập dữ liệu, thường được tính toán bằng phương pháp bình phương tối thiểu.
Tương tự hồi quy tuyến tính, hồi quy logistic cũng được sử dụng để ước tính mối quan hệ giữa một biến phụ thuộc và một hoặc nhiều biến độc lập. Tuy nhiên, hồi quy logistic được sử dụng để dự đoán biến phân loại thay vì biến liên tục. Biến phân loại có thể mang giá trị “đúng” hoặc “sai”, “có” hoặc “không”, “1” hoặc “0”, v.v.
Đơn vị đo lường của hồi quy logistic cũng khác so với hồi quy tuyến tính, vì nó tạo ra một giá trị xác suất. Chức năng logit giúp biến đổi đường cong hình chữ S thành một đường thẳng.
Mặc dù cả hai mô hình đều được sử dụng trong phân tích hồi quy để dự đoán kết quả trong tương lai, nhưng hồi quy tuyến tính thường dễ hiểu hơn.
Ngoài ra, hồi quy tuyến tính không yêu cầu kích thước mẫu lớn như hồi quy logistic, vì hồi quy logistic cần một mẫu đại diện đầy đủ cho tất cả các nhóm phản hồi. Nếu mẫu không đủ lớn hoặc không đại diện, mô hình có thể không có đủ sức mạnh thống kê để phát hiện tác động có ý nghĩa.
Ứng thực tế của Logistic Regression
Hồi quy logistic có nhiều ứng dụng thực tế trong các ngành công nghiệp khác nhau:
- Sản xuất: Các công ty sản xuất sử dụng phân tích hồi quy logistic để ước tính xác suất hỏng hóc của các bộ phận máy móc. Dựa trên xác suất này, họ có thể lên kế hoạch bảo trì để giảm thiểu sự cố trong tương lai, đảm bảo hoạt động sản xuất liên tục.
- Chăm sóc sức khỏe: Các nhà nghiên cứu y khoa sử dụng mô hình hồi quy logistic để dự đoán khả năng mắc bệnh của bệnh nhân, từ đó lên kế hoạch điều trị và chăm sóc dự phòng. Họ có thể so sánh ảnh hưởng của tiền sử gia đình hoặc yếu tố di truyền lên bệnh tật.
- Tài chính: Các công ty tài chính sử dụng hồi quy logistic để phân tích các giao dịch tài chính, phát hiện gian lận, đánh giá rủi ro tín dụng và rủi ro bảo hiểm. Các bài toán này phù hợp với hồi quy logistic vì kết quả thường là rời rạc (ví dụ: rủi ro cao/thấp, gian lận/không gian lận).
- Marketing (Tiếp thị): Các công cụ quảng cáo trực tuyến sử dụng mô hình hồi quy logistic để dự đoán khả năng người dùng nhấp vào quảng cáo. Nhờ đó, các nhà tiếp thị có thể phân tích phản ứng của người dùng với các thông điệp và hình ảnh khác nhau, tạo ra các chiến dịch quảng cáo hiệu quả, thu hút khách hàng.
Hồi quy logistic là một phương pháp phân tích dữ liệu mạnh mẽ, hỗ trợ doanh nghiệp và tổ chức đưa ra dự đoán chính xác trong nhiều lĩnh vực khác nhau. Với khả năng xử lý dữ liệu nhanh, dễ triển khai và phù hợp cho các bài toán phân loại, mô hình này trở thành lựa chọn phổ biến trong khoa học dữ liệu và trí tuệ nhân tạo.
Với sự phát triển của công nghệ và nhu cầu tính toán ngày càng cao, việc lựa chọn một giải pháp lưu trữ phù hợp đóng vai trò quan trọng trong việc vận hành các mô hình phân tích dữ liệu. Dịch vụ thuê VPS chất lượng giá rẻ tại InterData cung cấp hạ tầng phần cứng thế hệ mới, sử dụng CPU AMD EPYC/Intel Xeon Platinum mạnh mẽ, ổ cứng SSD NVMe U.2 tốc độ cao, đảm bảo hiệu suất tối ưu cho các tác vụ tính toán và xử lý dữ liệu lớn.
Nếu bạn cần một hệ thống lưu trữ mạnh mẽ hơn với khả năng mở rộng linh hoạt, dịch vụ thuê Cloud Server giá rẻ tốc độ cao là lựa chọn lý tưởng. Máy chủ sử dụng công nghệ điện toán đám mây tiên tiến, cho phép nâng cấp tài nguyên nhanh chóng, tối ưu dung lượng, băng thông cao, giúp vận hành các ứng dụng phân tích dữ liệu mượt mà, ổn định. Hãy liên hệ ngay để được tư vấn giải pháp phù hợp với nhu cầu của bạn!
INTERDATA
- Website: Interdata.vn
- Hotline: 1900-636822
- Email: [email protected]
- VPĐD: 240 Nguyễn Đình Chính, P.11. Q. Phú Nhuận, TP. Hồ Chí Minh
- VPGD: Số 211 Đường số 5, KĐT Lakeview City, P. An Phú, TP. Thủ Đức, TP. Hồ Chí Minh











