Quy trình quyết định Markov (MDP) là một công cụ quan trọng trong trí tuệ nhân tạo và học máy, giúp mô hình hóa quá trình ra quyết định trong các hệ thống động với sự không chắc chắn. Bằng cách sử dụng một cấu trúc toán học chính thức, MDP hỗ trợ các tác nhân đưa ra các quyết định tối ưu dựa trên trạng thái hiện tại và môi trường xung quanh. Bài viết này sẽ giúp bạn hiểu rõ MDP là gì, các thành phần cốt lõi của nó và ứng dụng thực tế trong các lĩnh vực như robot học, xử lý ngôn ngữ tự nhiên, và tối ưu hóa hệ thống.
Markov Decision Process – MDP là gì?
Quy trình quyết định Markov – Markov Decision Process (MDP) là một mô hình toán học mô tả quá trình ra quyết định trong một hệ thống động có tính ngẫu nhiên. MDP được dùng trong các tình huống mà kết quả có thể xảy ra một cách ngẫu nhiên hoặc bị chi phối bởi người ra quyết định, người phải đưa ra các lựa chọn tuần tự theo thời gian.
MDP giúp đánh giá hành động nào nên được thực hiện tại mỗi thời điểm, dựa trên trạng thái hiện tại và môi trường của hệ thống.
MDP hoạt động dựa trên các biến như môi trường, hành động của tác nhân (agent) và phần thưởng để xác định hành động tối ưu tiếp theo. Tùy vào tập hành động, trạng thái và tần suất ra quyết định, MDP được phân thành bốn loại: hữu hạn, vô hạn, liên tục hoặc rời rạc.
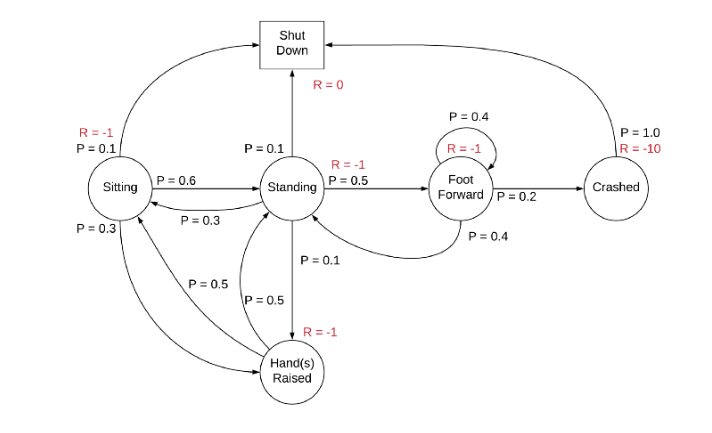
MDP xuất hiện từ những năm đầu thập niên 1950. Tên gọi “Markov” bắt nguồn từ nhà toán học người Nga Andrey Markov, người có đóng góp quan trọng trong việc phát triển lý thuyết quá trình ngẫu nhiên.
Ban đầu, MDP được ứng dụng để giải quyết các vấn đề như quản lý hàng tồn kho, tối ưu hóa xếp hàng và định tuyến. Ngày nay, MDP được dùng rộng rãi trong các lĩnh vực như: lập trình động, robot học, điều khiển tự động, kinh tế học, sản xuất và nhiều lĩnh vực kỹ thuật khác.
Trong trí tuệ nhân tạo (AI), MDP dùng để mô hình hóa các tình huống ra quyết định tuần tự có yếu tố xác suất. Mô hình này giúp thiết kế các tác nhân thông minh có thể hoạt động lâu dài trong môi trường mà kết quả của hành động có thể không chắc chắn.
MDP thường được ứng dụng nhiều trong hai nhánh chính của AI là lập kế hoạch xác suất (probabilistic planning) và học tăng cường (reinforcement learning – RL).
- Lập kế hoạch xác suất sử dụng mô hình đã biết để đạt được mục tiêu của tác nhân, đồng thời hướng dẫn máy hoặc hệ thống học cách hành xử phù hợp để đạt được kết quả mong muốn.
- Học tăng cường cho phép hệ thống học hỏi từ phản hồi (feedback) mà tác nhân nhận được từ môi trường.
Các thành phần cốt lõi của MDP
Một Quy trình Quyết định Markov (MDP) thường được định nghĩa thông qua một tập hợp các yếu tố cấu thành chính yếu sau đây:
Trạng thái (States – S)
States – S là tập hợp bao gồm tất cả các tình huống, hoàn cảnh hoặc cấu hình khả dĩ mà một tác nhân (agent) có thể đối mặt hoặc ở vào. Ví dụ minh họa bao gồm vị trí cụ thể của một con robot trong không gian một căn phòng, hoặc mức độ tồn kho hiện tại của một loại sản phẩm.
Hành động (Actions – A)
Actions – A bộ sưu tập tất cả các lựa chọn hay phương án mà tác nhân được phép thực hiện tại mỗi trạng thái. Chẳng hạn, đó có thể là tập hợp các hướng mà con robot có thể chọn để di chuyển, hoặc các quyết định về số lượng sản phẩm cần thiết để đặt hàng thêm.
Xác suất chuyển đổi trạng thái (Transition Probabilities – P)
Yếu tố Transition Probabilities – P biểu thị khả năng (xác suất) để hệ thống chuyển từ một trạng thái này sang một trạng thái khác, sau khi tác nhân đã tiến hành một hành động cụ thể. Nó phản ánh bản chất không chắc chắn hoặc tính ngẫu nhiên vốn có trong môi trường hoạt động.
Lấy ví dụ, nỗ lực di chuyển về phía trước của robot có thể đạt được mục tiêu với xác suất 90%, nhưng đồng thời cũng có 10% khả năng gặp thất bại (như là giữ nguyên vị trí cũ hoặc không may va chạm vào một chướng ngại vật).
Phần thưởng (Rewards – R)
Rewards – R là một tín hiệu có giá trị số mà tác nhân sẽ nhận được sau khi hoàn tất một hành động dẫn đến sự chuyển đổi từ trạng thái này sang trạng thái khác. Giá trị phần thưởng này cho biết mức độ “đáng mong đợi” hay “tích cực” của sự chuyển đổi đó xét về mặt lợi ích tức thời.
Mục tiêu tổng quát trong các bài toán MDP thường là tìm cách tối đa hóa tổng phần thưởng được tích lũy qua một khoảng thời gian dài.
Chính sách (Policy – π)
Chính sách (Policy – π) đại diện cho chiến lược hay phương cách hành động mà tác nhân tuân theo. Chính sách này xác định rõ hành động nào nên được lựa chọn khi tác nhân đang ở trong mỗi trạng thái cụ thể.
Mục tiêu chính yếu khi giải quyết một bài toán MDP thường là khám phá ra một “chính sách tối ưu” – tức là chiến lược giúp tối đa hóa tổng giá trị phần thưởng kỳ vọng có thể đạt được trong dài hạn.
Trong các môi trường có độ phức tạp cao, người ta thường vận dụng các kỹ thuật tiên tiến từ lĩnh vực Học tăng cường sâu (Deep Reinforcement Learning) để tìm ra những chính sách hiệu quả như vậy.
Mối quan hệ của MDP trong AI và Học máy (ML)
Quy trình Quyết định Markov (MDP) đóng vai trò cung cấp một khung khổ toán học chính thức để cấu trúc hóa các bài toán cho hầu hết những tác vụ thuộc lĩnh vực Học tăng cường (Reinforcement Learning – RL). Điều này khác biệt so với Học có giám sát (Supervised Learning), phương pháp học dựa trên dữ liệu đã được gán nhãn, và cũng khác với Học không giám sát (Unsupervised Learning), tập trung vào việc tìm kiếm các mẫu trong dữ liệu.
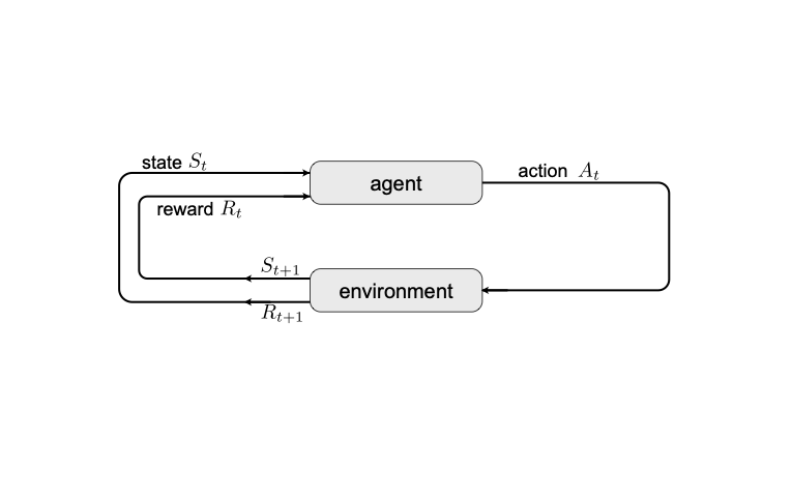
Học tăng cường (RL) lại chú trọng vào quá trình học hỏi thông qua sự tương tác trực tiếp với môi trường và dựa vào các tín hiệu phản hồi (cụ thể là phần thưởng) để hướng tới việc hoàn thành một mục tiêu dài hạn. Chính vì lẽ đó, MDP trở thành một khuôn khổ hết sức tự nhiên và phù hợp để mô tả các bài toán RL.
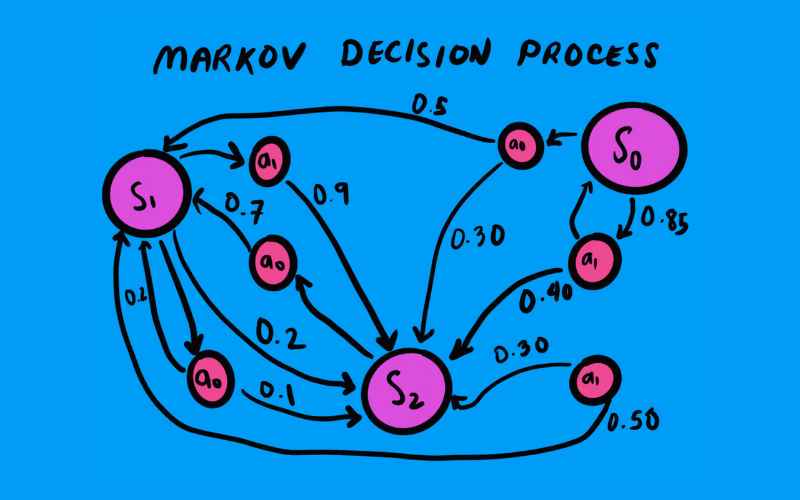
Khung mô hình MDP này có tầm quan trọng đặc biệt trong việc huấn luyện các tác nhân (agents) cần phải đưa ra một chuỗi các quyết định liên tiếp trong những môi trường hoạt động có tính chất động và thay đổi.
Sự liên quan của nó ngày càng trở nên rõ rệt và được ứng dụng nhiều hơn trong các lĩnh vực như Thị giác Máy tính (Computer Vision – CV), nhất là đối với những tác vụ đòi hỏi khả năng nhận thức chủ động hoặc tương tác tích cực với môi trường xung quanh.
Trong nhánh Học máy (Machine Learning – ML) này (tức Học tăng cường), mục tiêu chung thường là tối ưu hóa sự thành công của tác vụ hoặc Độ chính xác (Accuracy) trong dài hạn, điều này đạt được thông qua việc học cách tối đa hóa các tín hiệu phần thưởng mà tác nhân nhận được từ môi trường.
Các ví dụ về ứng dụng quy trình quyết định Markov (MDP)
MDP đóng vai trò quan trọng trong nhiều lĩnh vực như khoa học máy tính, kỹ thuật điện, sản xuất công nghiệp, nghiên cứu vận hành, tài chính – kinh tế và viễn thông. Dưới đây là một số ví dụ tiêu biểu:
Giải quyết các bài toán định tuyến
MDP được dùng để giải quyết các bài toán định tuyến, ví dụ như bài toán người giao hàng (Traveling Salesman Problem – TSP). Trong bài toán này:
- Người giao hàng là tác nhân (agent)
- Các tuyến đường có thể đi là tập hợp các hành động
- Chi phí mỗi tuyến là phần thưởng (hoặc chi phí)
- Mục tiêu là tìm ra chính sách tối ưu để giảm tổng chi phí chuyến đi.
Quản lý bảo trì và sửa chữa hệ thống động
MDP được áp dụng để quyết định các hành động như: không can thiệp, sửa chữa hoặc thay thế linh kiện trong các hệ thống động như xe hơi, xe buýt, xe tải – vốn xuống cấp theo thời gian. Bằng cách mô hình hóa bài toán này với MDP, hệ thống có thể chọn các hành động giúp giảm chi phí bảo trì trong suốt vòng đời sử dụng.
Thiết kế máy móc thông minh
Nhờ sự phát triển của AI và học máy, MDP được ứng dụng mạnh trong các hệ thống robot, phương tiện tự hành, và các hệ thống tự động phức tạp. Trong học tăng cường, MDP giúp máy móc học cách thực hiện nhiệm vụ một cách tự động.
Ví dụ, công ty DeepMind Technologies (thuộc Google) đã kết hợp MDP với mạng nơ-ron để huấn luyện hệ thống chơi các trò chơi Atari tốt hơn con người. DeepMind còn sử dụng MDP để phát triển AlphaGo – máy chơi cờ vây, cũng như huấn luyện robot mô phỏng học cách đi bộ và chạy.
Thiết kế trò chơi đố vui (quiz games)
MDP được dùng để xây dựng trò chơi đố vui theo từng cấp độ. Mỗi cấp sẽ có câu hỏi với phần thưởng tiền mặt. Người chơi có thể chọn tiếp tục hoặc dừng lại. Nếu dừng, họ giữ phần thưởng đã có. Nếu chơi tiếp và trả lời sai, họ mất hết. MDP giúp mô hình hóa quyết định “chơi tiếp” hay “dừng lại” sao cho phần thưởng nhận được là cao nhất.
Quản lý thời gian chờ đèn giao thông
MDP hỗ trợ xác định thời gian tối ưu bật/tắt đèn giao thông. Mục tiêu là tăng số xe đi qua ngã tư và giảm thời gian chờ đợi. Ví dụ, hệ thống có thể dùng cảm biến để biết số xe đang đến, từ đó quyết định nên giữ đèn đỏ, bật đèn xanh, hay thay đổi sau 2 hoặc 5 giây.
Xác định số bệnh nhân cần tiếp nhận trong bệnh viện
Mỗi ngày, bệnh viện cần quyết định số bệnh nhân có thể tiếp nhận, dựa trên:
- Số bệnh nhân đã nhập viện
- Số giường còn trống
- Số bệnh nhân hồi phục và xuất viện
MDP giúp bệnh viện tối ưu hoá số bệnh nhân được tiếp nhận và số người hồi phục trong khoảng thời gian cụ thể.
Ngoài các ví dụ nêu trên, MDP còn rất quan trọng trong việc tối ưu hóa giao thức viễn thông, tinh chỉnh chiến lược giao dịch chứng khoán và điều phối hàng đợi trong sản xuất công nghiệp.
Một số ứng dụng thực tế của Markov Decision Process – MDP
MDP có rất nhiều ứng dụng thực tế, đặc biệt là trong các hệ thống sử dụng lập trình động (dynamic programming) và các thuật toán đệ quy. Một số ứng dụng tiêu biểu bao gồm:
- Robot học (Robotics): Robot sử dụng học tăng cường sâu (deep reinforcement learning) để thực hiện các chuyển động phức tạp, ra quyết định và xử lý dữ liệu cảm biến đầu vào.
- Xử lý ngôn ngữ tự nhiên (Natural Language Processing): Học tăng cường sâu được dùng để huấn luyện các mô hình ngôn ngữ lớn, chẳng hạn như chatbot và hệ thống hội thoại thông minh.
- Ra quyết định trong xe tự hành: Học tăng cường giúp huấn luyện các phương tiện tự hành phản ứng và xử lý tình huống tương tự như con người khi tham gia giao thông.
- Đầu tư tài chính và bảo hiểm: MDP được ứng dụng để phân tích các chiến lược đầu tư hiện tại dựa trên những quyết định trong quá khứ, từ đó hỗ trợ việc hoạch định chiến lược tài chính hiệu quả hơn.
- Bảo trì và sửa chữa thiết bị: MDP giúp xây dựng mô hình đánh giá sự cố trong máy móc và đưa ra quyết định nên bảo trì hay thay thế thiết bị theo thời gian, nhằm tối ưu chi phí và hiệu suất hoạt động.
- Dịch tễ học và y tế công cộng: MDP có thể được sử dụng để mô hình hóa các đợt bùng phát dịch bệnh và hỗ trợ việc đưa ra quyết định dựa trên số ca nhiễm tại từng thời điểm cụ thể.
Ngoài ra, MDP tạo dựng nền tảng lý thuyết vững chắc, cho phép giải quyết hiệu quả hàng loạt các bài toán ra quyết định theo chuỗi (tuần tự) thường gặp trong thế giới thực. Dưới đây là một số ví dụ điển hình:
- Định vị và dẫn đường cho Robot: Trong lĩnh vực này, một robot tự hành cần phải xác định lộ trình di chuyển tối ưu để đi từ điểm xuất phát đến vị trí đích, đồng thời phải khéo léo né tránh các chướng ngại vật trên đường. Mô hình MDP được áp dụng như sau: các trạng thái (states) đại diện cho mọi vị trí và hướng di chuyển khả dĩ của robot; các hành động (actions) bao gồm các lệnh điều khiển chuyển động như “tiến về phía trước”, “rẽ trái”, “rẽ phải”; xác suất chuyển tiếp (transitions) phản ánh khả năng thực hiện thành công các lệnh di chuyển đó (ví dụ, robot có thể bị trượt hoặc lệch hướng); và phần thưởng (rewards) thường được thiết kế để có giá trị dương khi robot đạt được mục tiêu và giá trị âm khi xảy ra va chạm hoặc lãng phí thời gian. Nguyên tắc này không chỉ áp dụng cho robot đơn giản mà còn được mở rộng cho các hệ thống tự hành phức tạp hơn, ví dụ tiêu biểu là Xe tự hành (Self-driving cars).
- Quản lý Hàng tồn kho (Inventory Management): MDP giúp xác định chính sách đặt hàng sao cho tối ưu nhất đối với các sản phẩm có nhu cầu thị trường biến động và không chắc chắn. Trong bài toán này: các trạng thái (states) biểu thị các mức độ tồn kho khác nhau của sản phẩm; các hành động (actions) là quyết định về số lượng hàng hóa cần đặt thêm; quá trình chuyển đổi trạng thái (transitions) phụ thuộc vào yếu tố ngẫu nhiên là nhu cầu thực tế từ phía khách hàng; và hàm phần thưởng (rewards) được xây dựng để cân bằng giữa lợi ích thu được từ doanh thu bán hàng và các chi phí liên quan như chi phí đặt hàng và chi phí lưu trữ kho bãi. Phương pháp này đóng vai trò rất quan trọng trong các ứng dụng hiện đại, chẳng hạn như việc ứng dụng Trí tuệ nhân tạo (AI) để quản lý hàng tồn kho trong ngành bán lẻ một cách thông minh và hiệu quả hơn. Các công trình nghiên cứu học thuật chuyên sâu về việc áp dụng MDP cho các vấn đề quản lý có thể được tìm thấy trong lĩnh vực Nghiên cứu Vận hành (Operations Research).
- Chiến lược trong Trò chơi (Game Playing): Các tác nhân trí tuệ nhân tạo (AI agents) có thể được huấn luyện để học cách chơi các trò chơi phức tạp như cờ vua hoặc cờ vây một cách hiệu quả thông qua khuôn khổ MDP. Cụ thể: mỗi trạng thái (state) tương ứng với một thế cờ (cấu hình bàn cờ) tại một thời điểm nhất định; các hành động (actions) là tập hợp tất cả những nước đi hợp lệ mà tác nhân có thể thực hiện từ trạng thái đó; và phần thưởng (reward) thường được trao vào cuối ván chơi, với giá trị lớn dành cho bên chiến thắng. Thành tựu vang dội của DeepMind với chương trình AlphaGo chính là một minh chứng rõ ràng cho sức mạnh và tiềm năng to lớn của Học tăng cường (Reinforcement Learning – RL), vốn dựa trên nền tảng lý thuyết của MDP, trong các lĩnh vực đòi hỏi tư duy chiến lược và ra quyết định phức tạp như vậy.
Quy trình quyết định Markov (MDP) không chỉ đóng vai trò quan trọng trong việc tối ưu hóa quyết định trong môi trường có tính ngẫu nhiên mà còn là nền tảng cho các phương pháp học máy hiện đại.
Từ việc ứng dụng MDP trong các lĩnh vực khác nhau, MDP đã chứng tỏ vai trò thiết yếu trong nhiều lĩnh vực công nghệ. Hiểu MDP là gì và áp dụng nó có thể giúp giải quyết hiệu quả các vấn đề ra quyết định phức tạp, mở ra cơ hội lớn cho những tiến bộ trong các ứng dụng trí tuệ nhân tạo và học máy.
Khi triển khai các mô hình như Markov Decision Process (MDP) để tối ưu hóa quyết định trong hệ thống, việc sở hữu một hạ tầng mạnh mẽ là điều cần thiết. Tại InterData, bạn có thể thuê VPS chất lượng giá rẻ với phần cứng thế hệ mới như CPU AMD EPYC hoặc Intel Xeon Platinum, kết hợp SSD NVMe U.2 và băng thông cao, đáp ứng tốt các yêu cầu tính toán phức tạp cho các mô hình AI.
Nếu bạn cần một giải pháp linh hoạt và mạnh mẽ hơn, thuê Cloud Server giá rẻ tốc độ cao tại InterData sẽ là lựa chọn lý tưởng. Với dung lượng tối ưu và cấu hình mạnh mẽ, dịch vụ Cloud Server tại InterData giúp bạn xử lý hiệu quả các tác vụ học máy và trí tuệ nhân tạo, đảm bảo hiệu suất cao và ổn định cho các ứng dụng đòi hỏi tài nguyên lớn.
Liên hệ InterData ngay để được tư vấn và dùng thử dịch vụ!
INTERDATA
- Website: Interdata.vn
- Hotline: 1900-636822
- Email: [email protected]
- VPĐD: 240 Nguyễn Đình Chính, P.11. Q. Phú Nhuận, TP. Hồ Chí Minh
- VPGD: Số 211 Đường số 5, KĐT Lakeview City, P. An Phú, TP. Thủ Đức, TP. Hồ Chí Minh










