Hồi quy tuyến tính là một trong những khái niệm quan trọng và được ứng dụng rộng rãi nhất trong thống kê, phân tích dữ liệu và máy học. Nghe có vẻ phức tạp, nhưng thực tế hồi quy tuyến tính lại khá dễ hiểu. Bài viết này của InterData sẽ giải thích tất tần tật về hồi quy tuyến tính, từ định nghĩa, cách hoạt động, tầm quan trọng, đến các loại hồi quy tuyến tính và ứng dụng trong thực tế. Dù bạn là người mới bắt đầu hay đã có kinh nghiệm, bài viết này đều cung cấp thông tin hữu ích.
Hồi quy tuyến tính là gì?
Hồi quy tuyến tính (linear regression) là một phương pháp thống kê dùng để mô hình hóa mối quan hệ giữa một biến số phụ thuộc (biến mục tiêu) và một hoặc nhiều biến số độc lập (biến dự đoán) bằng một phương trình tuyến tính. Nói một cách đơn giản, nó giúp chúng ta “vẽ” một đường thẳng (hoặc mặt phẳng, siêu phẳng trong không gian nhiều chiều) phù hợp nhất với dữ liệu, để từ đó có thể dự đoán giá trị của biến phụ thuộc.
Để dễ hình dung, hãy tưởng tượng bạn đang cố gắng tìm hiểu xem chiều cao của một người (biến phụ thuộc) có liên quan như thế nào đến chiều dài bàn chân của họ (biến độc lập). Hồi quy tuyến tính sẽ giúp bạn tìm ra một phương trình, ví dụ: Chiều cao = 80 + 3.5 * Chiều dài bàn chân. Phương trình này cho thấy, trung bình, cứ mỗi cm chiều dài bàn chân tăng lên, chiều cao sẽ tăng thêm 3.5 cm. Dĩ nhiên, sẽ có những sai số nhất định, nhưng mô hình này cung cấp một cách xấp xỉ khá tốt.

Phương trình tổng quát của hồi quy tuyến tính (đơn biến) có dạng: y = β₀ + β₁x + ε. Trong đó, y là biến phụ thuộc, x là biến độc lập, β₀ là hệ số chặn (giá trị của y khi x = 0), β₁ là hệ số góc (cho biết mức độ thay đổi của y khi x thay đổi 1 đơn vị), và ε (epsilon) đại diện cho sai số ngẫu nhiên – phần mà mô hình không giải thích được.
Các nhà khoa học dữ liệu thường sử dụng phương pháp bình phương tối thiểu (Ordinary Least Squares – OLS) để tìm ra các hệ số β₀ và β₁ “tốt nhất”. “Tốt nhất” ở đây có nghĩa là các hệ số này làm cho tổng bình phương các sai số (sự khác biệt giữa giá trị thực tế và giá trị dự đoán) là nhỏ nhất.
Hồi quy tuyến tính không chỉ dừng lại ở một biến độc lập. Khi có nhiều biến độc lập (ví dụ: chiều cao không chỉ phụ thuộc vào chiều dài bàn chân mà còn phụ thuộc vào cân nặng, độ tuổi,…), chúng ta có hồi quy tuyến tính đa biến. Phương trình lúc này sẽ có dạng: y = β₀ + β₁x₁ + β₂x₂ + … + βₚxₚ + ε.
Một ví dụ thực tế khác: một công ty có thể sử dụng hồi quy tuyến tính để dự đoán doanh số bán hàng (biến phụ thuộc) dựa trên các yếu tố như chi phí quảng cáo, giá sản phẩm, và số lượng nhân viên bán hàng (các biến độc lập). Mô hình này giúp công ty đưa ra các quyết định kinh doanh hiệu quả hơn. Theo một nghiên cứu của Harvard Business Review, các công ty sử dụng phân tích dữ liệu (trong đó có hồi quy tuyến tính) có năng suất cao hơn 5-6% so với các đối thủ không sử dụng.
Tại sao hồi quy tuyến tính lại quan trọng?
Hồi quy tuyến tính là một công cụ quan trọng bậc nhất trong phân tích dữ liệu và thống kê vì nó cung cấp một phương pháp đơn giản, dễ hiểu và hiệu quả để mô hình hóa mối quan hệ giữa các biến số, từ đó đưa ra dự đoán và rút ra kết luận có giá trị.
Khả năng dự đoán
Một trong những lý do chính khiến hồi quy tuyến tính trở nên quan trọng là khả năng dự đoán giá trị của biến phụ thuộc. Ví dụ, một công ty bất động sản có thể sử dụng hồi quy tuyến tính để dự đoán giá nhà dựa trên diện tích, số phòng ngủ, vị trí và các yếu tố khác. Bằng cách xây dựng một mô hình hồi quy, công ty có thể đưa ra ước tính giá nhà chính xác hơn, giúp cả người mua và người bán đưa ra quyết định tốt hơn.
Hiểu rõ mối quan hệ giữa các biến
Hồi quy tuyến tính không chỉ giúp dự đoán, mà còn giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các biến số. Bằng cách xem xét các hệ số hồi quy, chúng ta có thể biết được biến độc lập nào có ảnh hưởng lớn nhất đến biến phụ thuộc, và ảnh hưởng đó là tích cực hay tiêu cực. Ví dụ, trong nghiên cứu y tế, hồi quy tuyến tính có thể được sử dụng để xác định các yếu tố nguy cơ gây bệnh tim mạch, chẳng hạn như huyết áp, mức cholesterol, và thói quen hút thuốc.
Tính đơn giản và dễ hiểu
So với các phương pháp học máy phức tạp hơn, hồi quy tuyến tính có ưu điểm là tương đối đơn giản và dễ hiểu. Điều này làm cho nó trở thành một công cụ lý tưởng cho những người mới bắt đầu làm quen với phân tích dữ liệu, cũng như cho các chuyên gia muốn giải thích kết quả của họ cho những người không có chuyên môn. Kết quả được thể hiện qua một phương trình dễ hình dung, có thể hiểu rõ ý nghĩa của từng hệ số.
Ứng dụng rộng rãi
Hồi quy tuyến tính có ứng dụng rộng rãi trong nhiều lĩnh vực, từ kinh doanh, tài chính, kinh tế, đến y học, kỹ thuật, khoa học xã hội, và nhiều lĩnh vực khác. Bất cứ nơi nào có dữ liệu và nhu cầu phân tích mối quan hệ giữa các biến, hồi quy tuyến tính đều có thể được sử dụng. Theo một khảo sát của KDnuggets, hồi quy tuyến tính là một trong ba phương pháp phân tích dữ liệu được sử dụng phổ biến nhất.
Nền tảng cho các phương pháp nâng cao
Hồi quy tuyến tính là nền tảng cho nhiều phương pháp phân tích dữ liệu và học máy nâng cao hơn. Việc hiểu rõ hồi quy tuyến tính sẽ giúp bạn dễ dàng tiếp cận và làm chủ các kỹ thuật phức tạp hơn, chẳng hạn như hồi quy logistic, hồi quy đa thức (Polynomial Regression), mô hình tuyến tính tổng quát (Generalized Linear Models – GLMs), và thậm chí cả các mạng nơ-ron (Neural Networks). Hiểu được nó giúp bạn có bước đệm tốt trong lĩnh vực này.
Hồi quy tuyến tính hoạt động như thế nào?
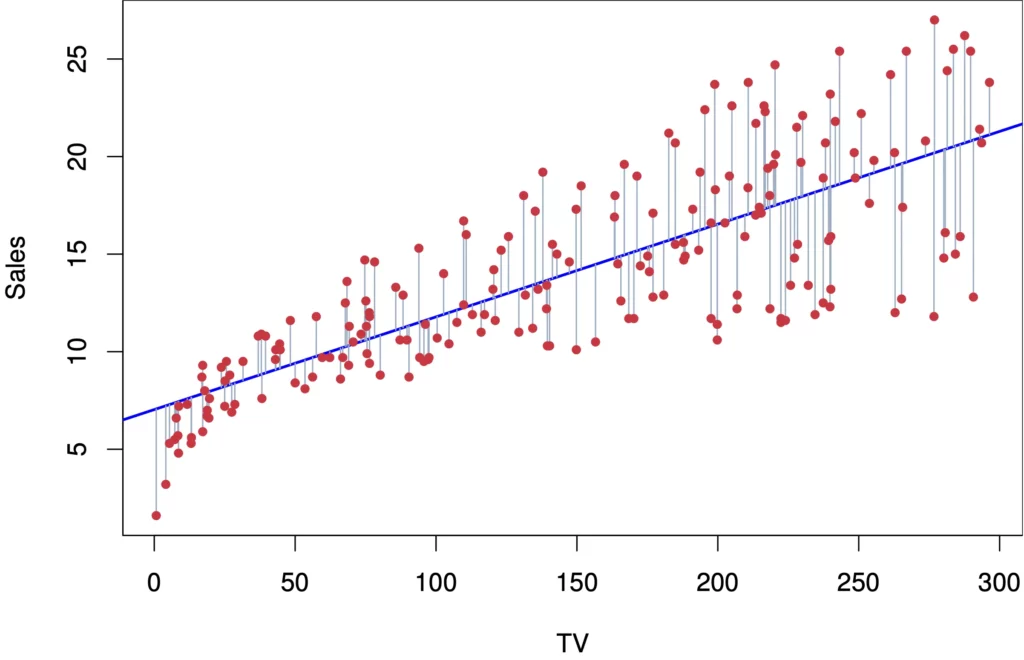
Hồi quy tuyến tính hoạt động bằng cách tìm ra một đường thẳng (hoặc mặt phẳng, siêu phẳng trong không gian nhiều chiều) phù hợp nhất với dữ liệu, sao cho tổng bình phương sai số giữa giá trị thực tế và giá trị dự đoán là nhỏ nhất. Đường thẳng này được xác định bởi một phương trình tuyến tính.
Hãy tưởng tượng bạn có một tập dữ liệu về chiều cao và cân nặng của một nhóm người. Bạn muốn tìm ra mối quan hệ giữa hai biến này. Hồi quy tuyến tính sẽ giúp bạn “vẽ” một đường thẳng trên biểu đồ phân tán (scatter plot) của dữ liệu, sao cho đường thẳng này “gần” với tất cả các điểm dữ liệu nhất có thể.
Phương trình của đường thẳng này có dạng: y = β₀ + β₁x + ε.
- y là biến phụ thuộc (cân nặng).
- x là biến độc lập (chiều cao).
- β₀ là hệ số chặn (giá trị của cân nặng khi chiều cao bằng 0 – một giá trị lý thuyết, không có ý nghĩa thực tế trong trường hợp này).
- β₁ là hệ số góc (cho biết cân nặng thay đổi bao nhiêu khi chiều cao thay đổi 1 đơn vị).
- ε là sai số (phần chênh lệch giữa giá trị thực tế và giá trị dự đoán).
Để tìm ra các hệ số β₀ và β₁ “tốt nhất”, hồi quy tuyến tính sử dụng phương pháp bình phương tối thiểu (Ordinary Least Squares – OLS). Phương pháp này sẽ tìm ra các giá trị của β₀ và β₁ sao cho tổng bình phương của các sai số (ε) là nhỏ nhất. Nói cách khác, nó tìm ra đường thẳng “gần” với tất cả các điểm dữ liệu nhất.
Ví dụ, giả sử sau khi thực hiện hồi quy tuyến tính, bạn tìm được phương trình: Cân nặng = -100 + 0.8 * Chiều cao. Điều này có nghĩa là:
- Khi chiều cao bằng 0 (một giá trị không thực tế), cân nặng ước tính là -100 kg (hệ số chặn β₀).
- Mỗi khi chiều cao tăng thêm 1 cm, cân nặng ước tính sẽ tăng thêm 0.8 kg (hệ số góc β₁).
- Phương trình trên sẽ có sai số vì trên thực tế sẽ không có mối liên hệ hoàn hảo.
Một khi đã có phương trình hồi quy, bạn có thể sử dụng nó để dự đoán cân nặng của một người dựa trên chiều cao của họ. Ví dụ, nếu một người cao 170 cm, bạn có thể dự đoán cân nặng của họ là: -100 + 0.8 * 170 = 36 kg. Tất nhiên, đây chỉ là một giá trị dự đoán, và giá trị thực tế có thể khác một chút.
Quan trọng cần lưu ý là hồi quy tuyến tính dựa trên một số giả định về dữ liệu. Ví dụ, mối quan hệ giữa các biến phải là tuyến tính, sai số phải có phân phối chuẩn, và không có hiện tượng đa cộng tuyến (trong trường hợp hồi quy đa biến). Nếu các giả định này bị vi phạm, kết quả của mô hình có thể không chính xác.
Hồi quy tuyến tính trong máy học là gì?
Trong máy học (Machine Learning), hồi quy tuyến tính là một thuật toán học có giám sát (Supervised Learning) cơ bản, được sử dụng để dự đoán một biến mục tiêu (biến phụ thuộc) có giá trị liên tục dựa trên một hoặc nhiều biến đầu vào (biến độc lập). Nó thuộc nhóm các bài toán hồi quy (Regression).
Nói một cách đơn giản, máy tính sẽ “học” từ dữ liệu huấn luyện (training data) để tìm ra mối quan hệ tuyến tính giữa các biến đầu vào và biến mục tiêu. Sau đó, mô hình đã học có thể được sử dụng để dự đoán giá trị của biến mục tiêu cho các dữ liệu mới.
Cách thức hoạt động
Quá trình “học” của thuật toán hồi quy tuyến tính trong máy học bao gồm các bước chính sau:
- Chuẩn bị dữ liệu: Thu thập và tiền xử lý dữ liệu, bao gồm làm sạch dữ liệu, xử lý các giá trị thiếu, và chuẩn hóa dữ liệu (nếu cần).
- Chọn mô hình: Chọn mô hình hồi quy tuyến tính (đơn biến hoặc đa biến, tùy thuộc vào số lượng biến đầu vào).
- Huấn luyện mô hình: Sử dụng dữ liệu huấn luyện để “huấn luyện” mô hình, tức là tìm ra các hệ số hồi quy (β₀, β₁, …, βₚ) sao cho hàm mất mát (loss function) – thường là tổng bình phương sai số (SSE) – là nhỏ nhất. Việc này thường được thực hiện bằng phương pháp bình phương tối thiểu (OLS) hoặc các phương pháp tối ưu hóa khác như Gradient Descent.
- Đánh giá mô hình: Sử dụng dữ liệu kiểm tra (test data) – dữ liệu mà mô hình chưa từng “nhìn thấy” – để đánh giá hiệu suất của mô hình. Các thước đo đánh giá thường dùng bao gồm R-squared, RMSE (Root Mean Squared Error), MAE (Mean Absolute Error),…
- Dự đoán: Sử dụng mô hình đã huấn luyện để dự đoán giá trị của biến mục tiêu cho các dữ liệu mới.
Ví dụ minh họa
Giả sử bạn muốn xây dựng một mô hình máy học để dự đoán giá nhà dựa trên diện tích. Bạn có dữ liệu về diện tích và giá của 100 căn nhà. Bạn sẽ chia dữ liệu này thành hai phần: 80 căn nhà dùng để huấn luyện mô hình, và 20 căn nhà còn lại dùng để kiểm tra mô hình.
Mô hình hồi quy tuyến tính sẽ “học” từ 80 căn nhà này để tìm ra phương trình: Giá nhà = β₀ + β₁ * Diện tích. Sau đó, bạn có thể sử dụng phương trình này để dự đoán giá của 20 căn nhà còn lại, và so sánh kết quả dự đoán với giá thực tế để đánh giá hiệu suất của mô hình.
Ưu điểm và nhược điểm
Ưu điểm:
- Đơn giản, dễ hiểu và dễ triển khai: Hồi quy tuyến tính là một trong những thuật toán máy học đơn giản nhất.
- Tốc độ huấn luyện nhanh: Thường không tốn nhiều thời gian để huấn luyện mô hình.
- Khả năng diễn giải cao: Các hệ số hồi quy cho biết mức độ ảnh hưởng của từng biến đầu vào đến biến mục tiêu.
Nhược điểm:
- Giả định về mối quan hệ tuyến tính: Chỉ hoạt động tốt khi mối quan hệ giữa các biến là tuyến tính.
- Nhạy cảm với dữ liệu ngoại lai (outliers): Các điểm dữ liệu ngoại lai có thể ảnh hưởng lớn đến kết quả của mô hình.
- Không thể mô hình hóa các mối quan hệ phức tạp: Không phù hợp cho các bài toán có mối quan hệ phi tuyến hoặc tương tác phức tạp giữa các biến.
Mối liên hệ với các khái niệm khác
Hồi quy tuyến tính có mối liên hệ chặt chẽ với nhiều khái niệm khác trong máy học và thống kê, chẳng hạn như:
- Học có giám sát (Supervised Learning): Hồi quy tuyến tính là một ví dụ điển hình của học có giám sát.
- Bài toán hồi quy (Regression Problem): Đây là loại bài toán mà hồi quy tuyến tính được sử dụng để giải quyết.
- Hàm mất mát (Loss Function): Đại lượng được sử dụng để đo lường mức độ “tốt” của mô hình.
- Gradient Descent: Một thuật toán tối ưu hóa thường được sử dụng để tìm các hệ số hồi quy.
- Hồi quy Ridge và Lasso: Các kỹ thuật mở rộng để tránh hiện tượng quá khớp (Overfitting).
|| Xem thêm: Trí tuệ nhân tạo (AI) là gì? Ứng dụng, Thách thức và Tương lai
Có những loại hồi quy tuyến tính nào?
Có hai loại hồi quy tuyến tính chính: hồi quy tuyến tính đơn biến (Simple Linear Regression) và hồi quy tuyến tính đa biến (Multiple Linear Regression). Ngoài ra, còn có một dạng mở rộng là hồi quy tuyến tính tổng quát (Generalized Linear Models – GLMs), nhưng dạng này phức tạp hơn và thường không được coi là “hồi quy tuyến tính” theo nghĩa cơ bản.
Hồi quy tuyến tính đơn biến (simple linear regression)
Đây là dạng đơn giản nhất của hồi quy tuyến tính, trong đó chỉ có một biến độc lập (x) và một biến phụ thuộc (y). Mối quan hệ giữa chúng được mô hình hóa bằng một đường thẳng.
Ví dụ: Dự đoán điểm thi cuối kỳ (y) dựa trên số giờ học (x). Phương trình hồi quy có dạng: Điểm thi = β₀ + β₁ * Số giờ học + ε.
Hồi quy tuyến tính đa biến (multiple linear regression)
Trong hồi quy tuyến tính đa biến, có nhiều biến độc lập (x₁, x₂, …, xₚ) cùng ảnh hưởng đến một biến phụ thuộc (y). Mối quan hệ này được mô hình hóa bằng một mặt phẳng (trong không gian ba chiều) hoặc siêu phẳng (trong không gian nhiều chiều hơn).
Ví dụ: Dự đoán giá nhà (y) dựa trên diện tích (x₁), số phòng ngủ (x₂), khoảng cách đến trung tâm thành phố (x₃). Phương trình hồi quy có dạng: Giá nhà = β₀ + β₁ * Diện tích + β₂ * Số phòng ngủ + β₃ * Khoảng cách + ε.
Điểm khác biệt chính:
- Số lượng biến độc lập: Đơn biến chỉ có một, đa biến có nhiều.
- Phương trình: Đơn biến là phương trình đường thẳng, đa biến là phương trình mặt phẳng hoặc siêu phẳng.
- Độ phức tạp: Đa biến phức tạp hơn về mặt tính toán và diễn giải.
- Vấn đề đa cộng tuyến: Trong hồi quy đa biến, cần chú ý đến hiện tượng đa cộng tuyến (multicollinearity), khi các biến độc lập có tương quan cao với nhau, làm cho kết quả hồi quy không ổn định.
Mối liên hệ: Hồi quy tuyến tính đơn biến có thể coi là một trường hợp đặc biệt của hồi quy tuyến tính đa biến, khi số lượng biến độc lập bằng 1.
Hồi quy tuyến tính tổng quát (GLMs)
Đây không hẳn là một “loại” hồi quy tuyến tính, mà là một họ các mô hình mở rộng, bao gồm cả hồi quy tuyến tính thông thường. Hồi quy Logistic (Logistic Regression), dù có chữ “hồi quy”, lại thuộc vào họ GLMs này, và được sử dụng cho bài toán phân loại (classification), chứ không phải hồi quy (dự đoán giá trị liên tục). Vì vậy, GLMs vượt ra ngoài phạm vi của “hồi quy tuyến tính” cơ bản.
Trong quá trình phân tích hồi quy tuyến tính, việc xử lý dữ liệu lớn và phức tạp đòi hỏi sức mạnh tính toán đáng kể. Nếu bạn đang tìm kiếm giải pháp để tăng tốc quá trình này, hãy cân nhắc thuê VPS chất lượng giá rẻ hoặc thuê Cloud Server giá rẻ tại InterData. Với phần cứng thế hệ mới, bộ xử lý AMD EPYC/Intel Platinum, SSD NVMe U.2 và băng thông cao, InterData mang đến cho bạn tốc độ xử lý vượt trội. Các gói dịch vụ có cấu hình mạnh mẽ, đáp ứng mọi nhu cầu tính toán của bạn với chi phí hợp lý.
Nếu bạn muốn tìm hiểu thêm về dịch vụ này, hãy liên hệ với InterData để được tư vấn chi tiết nhé!
INTERDATA
- Website: Interdata.vn
- Hotline: 1900-636822
- Email: [email protected]
- VPĐD: 240 Nguyễn Đình Chính, P.11. Q. Phú Nhuận, TP. Hồ Chí Minh
- VPGD: Số 211 Đường số 5, KĐT Lakeview City, P. An Phú, TP. Thủ Đức, TP. Hồ Chí Minh











