Trong lập trình, chúng ta thường xuyên đối mặt với những bài toán phức tạp. Để giải quyết chúng, các lập trình viên đã phát triển nhiều kỹ thuật và phương pháp khác nhau. Một trong những khái niệm nền tảng và mạnh mẽ, nhưng đôi khi cũng khá “hack não” cho người mới, chính là đệ quy (Recursion).
Bài viết này sẽ là kim chỉ nam giúp bạn hiểu rõ đệ quy là gì, từ định nghĩa cơ bản, cơ chế hoạt động, các ví dụ minh họa dễ hiểu bằng code, cho đến việc so sánh với vòng lặp quen thuộc, phân tích ưu nhược điểm và đưa ra lời khuyên khi nào nên sử dụng kỹ thuật này. Hãy cùng khám phá nhé!
Đệ quy (Recursion) là gì?
Đệ quy (Recursion) là một kỹ thuật lập trình cơ bản, trong đó một hàm (function) tự gọi lại chính nó để giải quyết vấn đề. Kỹ thuật này hiệu quả khi chia một bài toán lớn thành các bài toán con nhỏ hơn, giống hệt bài toán gốc nhưng với phạm vi hoặc dữ liệu đầu vào đơn giản hơn.

Điểm cốt lõi của đệ quy là việc hàm tự thực hiện lại chính nó. Mỗi lần gọi lại này sẽ xử lý một phần nhỏ của bài toán tổng thể. Quá trình này tiếp diễn cho đến khi đạt được một điều kiện dừng cụ thể, giúp hàm không gọi lại chính nó vô hạn, tránh gây lỗi chương trình.
Bạn có thể hình dung đệ quy giống như những con búp bê Nga Matryoshka lồng vào nhau. Để mở con búp bê lớn nhất, bạn cần mở lần lượt các con nhỏ hơn bên trong. Mỗi hành động mở một con búp bê tương tự như một bước gọi đệ quy, giải quyết phiên bản nhỏ hơn của “bài toán mở búp bê”.
Mọi hàm đệ quy hoạt động đúng cần có hai thành phần thiết yếu. Một là Trường hợp cơ sở (Base Case): đây là điều kiện cụ thể mà tại đó hàm sẽ ngừng gọi lại chính nó và trả về một giá trị. Hai là Bước đệ quy (Recursive Step): nơi hàm gọi lại chính nó với dữ liệu đã được thay đổi để tiến gần hơn tới Trường hợp cơ sở.
Đệ quy cung cấp một cách tiếp cận khác so với việc sử dụng vòng lặp (iteration), ví dụ như vòng lặp for hoặc while, để thực hiện các công việc lặp đi lặp lại. Lựa chọn giữa chúng thường phụ thuộc vào bài toán cụ thể, sự rõ ràng của mã nguồn và đôi khi là hiệu suất mong muốn.
Kỹ thuật đệ quy tỏ ra đặc biệt mạnh mẽ và tự nhiên đối với các bài toán có bản chất đệ quy. Ví dụ điển hình bao gồm việc tính giai thừa, xử lý dãy Fibonacci, duyệt các cấu trúc dữ liệu (data structures) dạng cây, hoặc triển khai các giải thuật (algorithms) theo phương pháp chia để trị (divide and conquer).
Cơ chế hoạt động chi tiết của Hàm đệ quy
Để hiểu rõ hàm đệ quy hoạt động thế nào, chúng ta cần xem xét kỹ hai thành phần cốt lõi đã đề cập: Trường hợp cơ sở (Base Case) và Bước đệ quy (Recursive Step). Sự phối hợp nhịp nhàng giữa hai yếu tố này chính là chìa khóa cho một giải thuật đệ quy chính xác và hiệu quả.
Việc thiếu một trong hai thành phần, hoặc định nghĩa chúng không chính xác, sẽ dẫn đến lỗi. Nếu thiếu Base Case, hàm sẽ gọi lại chính nó mãi mãi (hoặc cho đến khi bộ nhớ cạn kiệt). Nếu Recursive Step không hướng đến Base Case, hàm cũng sẽ không bao giờ dừng lại đúng cách.
Trường hợp cơ sở (Base Case): Điểm dừng chân an toàn
Trường hợp cơ sở (Base Case) là điều kiện cụ thể trong hàm đệ quy mà tại đó, hàm sẽ không thực hiện lời gọi đệ quy nào nữa, thay vào đó nó trả về một giá trị kết quả trực tiếp. Đây chính là điểm dừng, là lối thoát của quá trình đệ quy, đảm bảo hàm kết thúc.
Sự tồn tại của Base Case là bắt buộc. Nếu không có nó, hàm sẽ liên tục gọi lại chính mình, tạo ra một chuỗi lời gọi vô hạn. Điều này nhanh chóng làm cạn kiệt bộ nhớ dành cho việc quản lý các lời gọi hàm, dẫn đến lỗi Stack Overflow (sẽ giải thích kỹ hơn ở phần sau).
Thường thì, Base Case tương ứng với trường hợp đơn giản nhất của bài toán, nơi mà kết quả có thể được xác định ngay lập tức mà không cần thêm bước đệ quy nào. Ví dụ, trong bài toán tính giai thừa n!, Base Case là 0! = 1. Với dãy Fibonacci, Base Cases là Fib(0) = 0 và Fib(1) = 1.
Khi thiết kế một hàm đệ quy, việc đầu tiên và quan trọng nhất là xác định (các) trường hợp cơ sở. Hãy tự hỏi: “Phiên bản đơn giản nhất của bài toán này là gì mà tôi có thể trả lời ngay lập tức?”. Câu trả lời sẽ giúp bạn định nghĩa Base Case một cách chính xác.
Bước đệ quy (Recursive Step): Hành trình chia nhỏ vấn đề
Bước đệ quy (Recursive Step) là phần của hàm nơi nó thực hiện lời gọi lại chính mình, nhưng với một phiên bản nhỏ hơn hoặc đơn giản hơn của bài toán ban đầu. Mục tiêu là để dữ liệu đầu vào tiến dần đến Trường hợp cơ sở (Base Case) sau mỗi lần gọi.
Trong bước này, hàm thường thực hiện một số phép tính hoặc xử lý dữ liệu, sau đó kết hợp kết quả đó với kết quả trả về từ lời gọi đệ quy tiếp theo. Lời gọi đệ quy này sử dụng các tham số đã được điều chỉnh (ví dụ: n-1 thay vì n) để đảm bảo bài toán đang được “thu nhỏ” lại.
Điều cực kỳ quan trọng là mỗi bước đệ quy phải đảm bảo rằng nó đang di chuyển “gần hơn” đến Base Case. Nếu bước đệ quy không làm thay đổi đầu vào theo hướng tiến đến Base Case, hàm sẽ không bao giờ đạt được điểm dừng và gây ra vòng lặp vô hạn (tương tự như thiếu Base Case).
Bước đệ quy chính là nơi thể hiện rõ tư duy chia để trị (divide and conquer). Thay vì giải quyết trực tiếp bài toán lớn, chúng ta chia nó thành một hoặc nhiều bài toán con giống hệt nhưng nhỏ hơn, giải quyết các bài toán con đó bằng cách gọi đệ quy, và cuối cùng kết hợp kết quả lại.
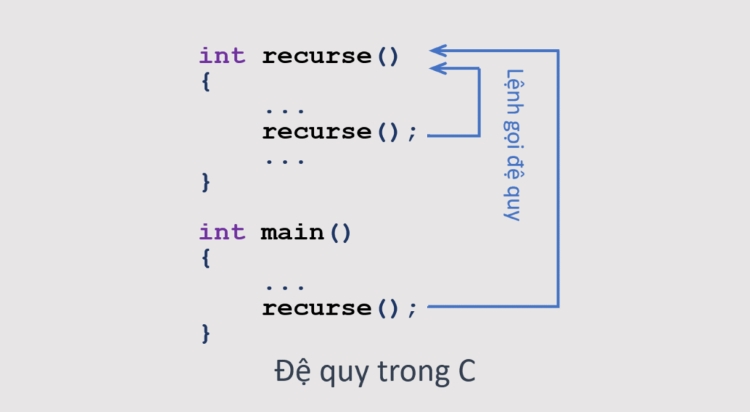
Ví dụ về Đệ quy trong Lập trình (Code dễ hiểu)
Lý thuyết sẽ dễ hình dung hơn rất nhiều qua các ví dụ thực tế. Chúng ta sẽ cùng xem xét một số bài toán kinh điển thường được giải bằng đệ quy, với code minh họa bằng Python và JavaScript – hai ngôn ngữ phổ biến và có cú pháp tương đối dễ đọc cho người mới bắt đầu.
Ví dụ 1: Tính Giai thừa (Factorial)
Bài toán tính giai thừa của một số nguyên không âm n, ký hiệu là n!, là một ví dụ nhập môn kinh điển cho đệ quy. Giai thừa được định nghĩa là tích của tất cả các số nguyên dương từ 1 đến n.
- Công thức:
n! = n * (n-1) * (n-2) * ... * 1 - Trường hợp cơ sở (Base Case):
0! = 1 - Bước đệ quy (Recursive Step):
n! = n * (n-1)!(với n > 0)
Python
# Code Python tính giai thừa bằng đệ quy
def factorial_recursive(n):
# Trường hợp cơ sở
if n == 0:
return 1
# Bước đệ quy
else:
return n * factorial_recursive(n - 1)
# Ví dụ sử dụng
print(f"3! = {factorial_recursive(3)}") # Output: 3! = 6
print(f"5! = {factorial_recursive(5)}") # Output: 5! = 120
JavaScript
// Code JavaScript tính giai thừa bằng đệ quy
function factorialRecursive(n) {
// Trường hợp cơ sở
if (n === 0) {
return 1;
}
// Bước đệ quy
else {
return n * factorialRecursive(n - 1);
}
}
// Ví dụ sử dụng
console.log(`3! = ${factorialRecursive(3)}`); // Output: 3! = 6
console.log(`5! = ${factorialRecursive(5)}`); // Output: 5! = 120
Trong đoạn code trên, hàm factorial_recursive kiểm tra nếu n bằng 0 (Base Case), nó trả về 1. Nếu không, nó trả về n nhân với kết quả của việc gọi lại chính nó với n-1 (Recursive Step), đưa bài toán tiến gần hơn đến Base Case n=0.
Hãy xem cách nó hoạt động với n=3:
factorial_recursive(3)gọifactorial_recursive(2). Nó chờ kết quả và sẽ nhân với 3.factorial_recursive(2)gọifactorial_recursive(1). Nó chờ kết quả và sẽ nhân với 2.factorial_recursive(1)gọifactorial_recursive(0). Nó chờ kết quả và sẽ nhân với 1.factorial_recursive(0)gặp Base Case, trả về 1.factorial_recursive(1)nhận được 1, tính 1 * 1 = 1, trả về 1.factorial_recursive(2)nhận được 1, tính 2 * 1 = 2, trả về 2.factorial_recursive(3)nhận được 2, tính 3 * 2 = 6, trả về 6. Kết quả cuối cùng là 6.
Ví dụ 2: Tính số Fibonacci thứ n
Dãy Fibonacci là một dãy số trong đó mỗi số là tổng của hai số liền trước nó. Dãy thường bắt đầu bằng 0 và 1.
- Định nghĩa:
Fib(n) = Fib(n-1) + Fib(n-2) - Trường hợp cơ sở (Base Cases):
Fib(0) = 0,Fib(1) = 1 - Bước đệ quy (Recursive Step):
Fib(n) = Fib(n-1) + Fib(n-2)(với n > 1)
Python
# Code Python tính số Fibonacci thứ n bằng đệ quy
def fibonacci_recursive(n):
# Các trường hợp cơ sở
if n <= 0:
return 0
elif n == 1:
return 1
# Bước đệ quy
else:
return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2)
# Ví dụ sử dụng
print(f"Fib(6) = {fibonacci_recursive(6)}") # Output: Fib(6) = 8
print(f"Fib(10) = {fibonacci_recursive(10)}") # Output: Fib(10) = 55
JavaScript
// Code JavaScript tính số Fibonacci thứ n bằng đệ quy
function fibonacciRecursive(n) {
// Các trường hợp cơ sở
if (n <= 0) {
return 0;
} else if (n === 1) {
return 1;
}
// Bước đệ quy
else {
return fibonacciRecursive(n - 1) + fibonacciRecursive(n - 2);
}
}
// Ví dụ sử dụng
console.log(`Fib(6) = ${fibonacciRecursive(6)}`); // Output: Fib(6) = 8
console.log(`Fib(10) = ${fibonacciRecursive(10)}`); // Output: Fib(10) = 55
Hàm fibonacci_recursive có hai Base Cases cho n=0 và n=1. Nếu n > 1, hàm gọi lại chính nó hai lần: một lần cho n-1 và một lần cho n-2, sau đó cộng kết quả của hai lời gọi đó lại.
Hãy xem xét fibonacci_recursive(4):
fib(4)gọifib(3)vàfib(2).fib(3)gọifib(2)vàfib(1)(trả về 1).fib(2)(lần 1, từ fib(3)) gọifib(1)(trả về 1) vàfib(0)(trả về 0). Nó tính 1 + 0 = 1, trả về 1.fib(3)nhận được 1 (từ fib(2)) và 1 (từ fib(1)), tính 1 + 1 = 2, trả về 2.fib(2)(lần 2, từ fib(4)) gọifib(1)(trả về 1) vàfib(0)(trả về 0). Nó tính 1 + 0 = 1, trả về 1.fib(4)nhận được 2 (từ fib(3)) và 1 (từ fib(2)), tính 2 + 1 = 3, trả về 3. Kết quả cuối cùng là 3.
Lưu ý quan trọng: Cách giải đệ quy này cho Fibonacci rất trực quan nhưng lại không hiệu quả. Bạn có thể thấy fib(2) được tính toán nhiều lần. Với n lớn hơn, số lần tính toán trùng lặp tăng lên theo cấp số nhân, làm chậm chương trình đáng kể. Các kỹ thuật như memoization hoặc dynamic programming (quy hoạch động) thường được dùng để tối ưu hóa.
Ví dụ 3: Đệ quy trong bài toán Tháp Hà Nội (Tower of Hanoi)
Tháp Hà Nội là một trò chơi toán học nổi tiếng, bao gồm ba cọc và một số đĩa có kích thước khác nhau có thể trượt lên bất kỳ cọc nào. Câu đố bắt đầu với các đĩa được xếp chồng lên nhau theo thứ tự kích thước giảm dần trên một cọc (cọc nguồn), sao cho đĩa nhỏ nhất ở trên cùng.
Mục tiêu là di chuyển toàn bộ chồng đĩa sang một cọc khác (cọc đích), tuân theo các quy tắc đơn giản sau:
- Mỗi lần chỉ được di chuyển một đĩa.
- Một đĩa chỉ có thể được di chuyển nếu nó là đĩa trên cùng của một chồng.
- Không được đặt đĩa lớn hơn lên trên đĩa nhỏ hơn.
Bài toán này có lời giải đệ quy rất thanh lịch. Để di chuyển n đĩa từ cọc Nguồn (A) sang cọc Đích (C), sử dụng cọc Trung gian (B):
- Di chuyển
n-1đĩa từ A sang B, sử dụng C làm trung gian. (Bước đệ quy) - Di chuyển đĩa thứ
n(đĩa lớn nhất) từ A sang C. (Hành động cơ bản) - Di chuyển
n-1đĩa từ B sang C, sử dụng A làm trung gian. (Bước đệ quy)
- Trường hợp cơ sở (Base Case): Khi
n = 0(không có đĩa nào để di chuyển), không làm gì cả.
Python
# Code Python giải bài toán Tháp Hà Nội bằng đệ quy
def tower_of_hanoi(n, source, destination, auxiliary):
# Trường hợp cơ sở
if n == 1:
print(f"Di chuyển đĩa 1 từ {source} sang {destination}")
return
# Bước đệ quy
# 1. Di chuyển n-1 đĩa từ nguồn sang trung gian
tower_of_hanoi(n - 1, source, auxiliary, destination)
# 2. Di chuyển đĩa lớn nhất từ nguồn sang đích
print(f"Di chuyển đĩa {n} từ {source} sang {destination}")
# 3. Di chuyển n-1 đĩa từ trung gian sang đích
tower_of_hanoi(n - 1, auxiliary, destination, source)
# Ví dụ sử dụng với 3 đĩa
n_disks = 3
print(f"Các bước di chuyển {n_disks} đĩa từ A sang C:")
tower_of_hanoi(n_disks, 'A', 'C', 'B')
JavaScript
// Code JavaScript giải bài toán Tháp Hà Nội bằng đệ quy
function towerOfHanoi(n, source, destination, auxiliary) {
// Trường hợp cơ sở (thay vì n=0, ta dừng khi n=1 và thực hiện di chuyển)
if (n === 1) {
console.log(`Di chuyển đĩa 1 từ ${source} sang ${destination}`);
return;
}
// Bước đệ quy
// 1. Di chuyển n-1 đĩa từ nguồn sang trung gian
towerOfHanoi(n - 1, source, auxiliary, destination);
// 2. Di chuyển đĩa lớn nhất từ nguồn sang đích
console.log(`Di chuyển đĩa ${n} từ ${source} sang ${destination}`);
// 3. Di chuyển n-1 đĩa từ trung gian sang đích
towerOfHanoi(n - 1, auxiliary, destination, source);
}
// Ví dụ sử dụng với 3 đĩa
const nDisks = 3;
console.log(`Các bước di chuyển ${nDisks} đĩa từ A sang C:`);
towerOfHanoi(nDisks, 'A', 'C', 'B');
Hàm tower_of_hanoi nhận số lượng đĩa n và tên của ba cọc. Base Case là khi chỉ còn 1 đĩa, ta chỉ cần di chuyển nó trực tiếp. Bước đệ quy thực hiện chính xác ba bước logic đã nêu: hai lời gọi đệ quy để di chuyển n-1 đĩa và một hành động di chuyển đĩa lớn nhất ở giữa.
Bài toán Tháp Hà Nội là một minh chứng tuyệt vời cho thấy đệ quy có thể diễn đạt lời giải cho một số vấn đề phức tạp một cách ngắn gọn và tự nhiên, phản ánh đúng cấu trúc của bài toán.
Đệ quy và Ngăn xếp lời gọi hàm (Call Stack)
Hoạt động của đệ quy gắn liền với một cấu trúc dữ liệu quan trọng trong bộ nhớ (memory) của máy tính: Ngăn xếp lời gọi hàm (Call Stack). Hiểu về Call Stack giúp làm sáng tỏ cách đệ quy thực sự hoạt động “bên trong” và tại sao lại có lỗi Stack Overflow.
Call Stack là một cấu trúc dữ liệu dạng ngăn xếp (Stack), hoạt động theo nguyên tắc LIFO (Last-In, First-Out – Vào sau, Ra trước). Mỗi khi một hàm được gọi trong chương trình, một “khung” (stack frame) mới chứa thông tin về lời gọi hàm đó sẽ được đẩy (push) lên đỉnh của Call Stack.
Khung ngăn xếp này lưu trữ các thông tin quan trọng như: các biến cục bộ của hàm, các tham số truyền vào, và địa chỉ trả về (nơi chương trình sẽ tiếp tục thực thi sau khi hàm này kết thúc). Khi một hàm thực hiện xong và trả về kết quả, khung ngăn xếp tương ứng của nó sẽ được lấy ra (pop) khỏi đỉnh Call Stack.
Trong trường hợp hàm đệ quy, mỗi lần hàm gọi lại chính nó, một khung ngăn xếp mới lại được đẩy lên Call Stack. Ví dụ, khi gọi factorial_recursive(3):
- Khung cho
factorial_recursive(3)được đẩy vào stack. - Nó gọi
factorial_recursive(2), khung chofactorial_recursive(2)được đẩy lên trên. - Nó gọi
factorial_recursive(1), khung chofactorial_recursive(1)được đẩy lên trên. - Nó gọi
factorial_recursive(0), khung chofactorial_recursive(0)được đẩy lên trên. factorial_recursive(0)gặp Base Case, trả về 1. Khung của nó được pop ra.factorial_recursive(1)nhận kết quả, tính toán, trả về 1. Khung của nó được pop ra.factorial_recursive(2)nhận kết quả, tính toán, trả về 2. Khung của nó được pop ra.factorial_recursive(3)nhận kết quả, tính toán, trả về 6. Khung của nó được pop ra. Stack trở lại trạng thái ban đầu.
Điều gì xảy ra nếu hàm đệ quy gọi chính nó quá nhiều lần mà không đạt đến trường hợp cơ sở? Hoặc nếu Base Case bị định nghĩa sai và không bao giờ đạt được? Mỗi lời gọi đệ quy sẽ tiếp tục đẩy thêm một khung mới vào Call Stack.
Call Stack, giống như mọi vùng nhớ khác, có kích thước giới hạn. Khi số lượng khung ngăn xếp bị đẩy vào vượt quá dung lượng cho phép của Call Stack, chương trình sẽ không còn đủ bộ nhớ để quản lý thêm lời gọi hàm nào nữa. Lúc này, một lỗi nghiêm trọng xảy ra, gọi là Stack Overflow (Tràn bộ nhớ stack), và chương trình thường sẽ bị dừng đột ngột.
Vì vậy, hiểu rõ mối liên hệ giữa đệ quy và Call Stack là cực kỳ quan trọng. Nó không chỉ giúp bạn hình dung cách đệ quy hoạt động mà còn giúp nhận biết và gỡ lỗi các vấn đề liên quan đến đệ quy sâu hoặc vô hạn, đặc biệt là lỗi Stack Overflow phổ biến.
So sánh Đệ quy (Recursion) và Vòng lặp (Iteration)
Đệ quy và vòng lặp (iteration) (sử dụng các cấu trúc như for, while) là hai cách chính để thực hiện các tác vụ lặp đi lặp lại trong lập trình. Mặc dù chúng có thể được sử dụng để giải quyết cùng một loại bài toán, chúng hoạt động theo những cách rất khác nhau. Việc hiểu rõ sự khác biệt giúp lập trình viên lựa chọn công cụ phù hợp.
Về logic thực thi, đệ quy giải quyết bài toán bằng cách gọi lại chính nó với các phiên bản nhỏ hơn cho đến khi đạt Base Case. Trong khi đó, vòng lặp thực hiện lặp lại một khối mã dựa trên một điều kiện lặp và thường sử dụng các biến đếm hoặc biến trạng thái để kiểm soát quá trình lặp.
Quản lý trạng thái cũng khác biệt. Đệ quy quản lý trạng thái của các bước trung gian một cách ngầm định thông qua các khung trên Call Stack (mỗi khung lưu trữ trạng thái của một lần gọi). Vòng lặp đòi hỏi lập trình viên phải quản lý trạng thái một cách tường minh thông qua các biến được cập nhật trong mỗi lần lặp.
Về cấu trúc code, hàm đệ quy thường có vẻ ngắn gọn và thanh lịch hơn đối với các bài toán có cấu trúc đệ quy tự nhiên (như duyệt cây). Code vòng lặp đôi khi có thể dài hơn nhưng luồng thực thi thường tuần tự và dễ theo dõi hơn đối với một số người.
Sử dụng bộ nhớ là một điểm khác biệt lớn. Mỗi lời gọi đệ quy tiêu tốn thêm không gian trên Call Stack. Nếu đệ quy quá sâu, nguy cơ Stack Overflow là rất cao. Vòng lặp thường chỉ sử dụng một lượng bộ nhớ tương đối cố định (cho các biến lặp), ít rủi ro về tràn bộ nhớ stack hơn nhiều.
Về hiệu suất, các lời gọi hàm trong đệ quy thường đi kèm với chi phí (overhead) nhất định, có thể làm cho đệ quy chậm hơn so với vòng lặp tương đương, đặc biệt với các tác vụ đơn giản. Vòng lặp thường có hiệu suất tốt hơn trong những trường hợp này. Tuy nhiên, cần lưu ý về kỹ thuật Tối ưu hóa Đệ quy Đuôi (Tail Call Optimization – TCO) có thể giúp loại bỏ overhead này trong một số ngôn ngữ/trình biên dịch (sẽ nói thêm ở phần FAQ).
Khả năng đọc và gỡ lỗi (debug) khá chủ quan. Code đệ quy có thể rất dễ đọc nếu bạn hiểu rõ logic đệ quy và bài toán phù hợp. Tuy nhiên, việc debug đệ quy có thể phức tạp hơn do phải theo dõi nhiều ngữ cảnh hàm trên Call Stack. Code vòng lặp thường dễ debug hơn vì luồng thực thi tuyến tính hơn.
Bảng tóm tắt so sánh:
| Tiêu chí | Đệ quy (Recursion) | Vòng lặp (Iteration) |
|---|---|---|
| Logic | Gọi lại chính hàm, có Base Case & Recursive Step | Lặp lại khối mã dựa trên điều kiện, dùng biến trạng thái |
| Quản lý trạng thái | Ngầm định qua Call Stack | Tường minh qua các biến lặp |
| Code | Thường ngắn gọn, thanh lịch cho bài toán phù hợp | Có thể dài hơn, luồng thực thi tuần tự hơn |
| Bộ nhớ | Tốn bộ nhớ Stack, nguy cơ Stack Overflow cao | Thường tốn ít bộ nhớ hơn, ít nguy cơ tràn Stack |
| Hiệu suất | Có thể chậm hơn do overhead gọi hàm | Thường nhanh hơn cho các tác vụ đơn giản |
| Debug | Có thể khó hơn do Call Stack phức tạp | Thường dễ hơn do luồng tuyến tính |
Ưu điểm và nhược điểm của việc sử dụng Đệ quy
Như mọi công cụ lập trình khác, đệ quy có những điểm mạnh và điểm yếu riêng. Hiểu rõ chúng giúp bạn đưa ra quyết định sáng suốt về việc có nên áp dụng kỹ thuật này vào giải pháp của mình hay không.
Ưu điểm của Đệ quy:
- Code rõ ràng và thanh lịch: Đối với các bài toán có cấu trúc vốn đã mang tính đệ quy (như làm việc với cây, đồ thị, các bài toán chia để trị như Quicksort, Mergesort), việc sử dụng đệ quy thường dẫn đến mã nguồn ngắn gọn, dễ đọc và thể hiện logic của giải thuật một cách tự nhiên hơn so với dùng vòng lặp.
- Giảm độ phức tạp của code (đôi khi): Trong một số trường hợp, việc triển khai bằng đệ quy có thể đơn giản hơn, cần ít biến trạng thái tạm thời hơn so với việc phải quản lý chúng một cách tường minh trong vòng lặp.
Nhược điểm của Đệ quy:
- Tiêu tốn bộ nhớ: Đây là nhược điểm lớn nhất. Mỗi lời gọi đệ quy tạo ra một khung mới trên Call Stack. Với độ sâu đệ quy lớn, lượng bộ nhớ tiêu thụ có thể tăng lên đáng kể, dẫn đến nguy cơ Stack Overflow, đặc biệt trong các môi trường có giới hạn bộ nhớ stack chặt chẽ.
- Hiệu suất thấp hơn (thường): Chi phí (overhead) liên quan đến việc gọi và trả về từ hàm có thể làm cho đệ quy chậm hơn so với một giải pháp vòng lặp tương đương cho cùng một bài toán, đặc biệt là khi các phép tính trong mỗi bước là đơn giản.
- Khó debug hơn: Việc theo dõi luồng thực thi qua nhiều cấp độ của Call Stack có thể phức tạp hơn so với việc theo dõi các biến thay đổi trong một vòng lặp. Hiểu cách hoạt động của Call Stack là điều cần thiết khi gỡ lỗi code đệ quy.
- Nguy cơ tính toán dư thừa: Các giải thuật đệ quy được thiết kế không cẩn thận (như ví dụ Fibonacci cơ bản) có thể dẫn đến việc tính toán lại cùng một giá trị nhiều lần, gây lãng phí tài nguyên nghiêm trọng.
Tóm lại, đệ quy là một công cụ mạnh mẽ và thanh lịch, nhưng cần được sử dụng một cách cân nhắc, đặc biệt chú ý đến các yếu tố về bộ nhớ và hiệu suất.
CÓ THỂ BẠN QUAN TÂM
Khi cần môi trường ổn định để thực hành, kiểm thử hiệu năng thuật toán như đệ quy, hay triển khai ứng dụng, bạn có thể tham khảo dịch vụ thuê VPS giá rẻ – uy tín – tốc độ cao tại InterData. Chỉ từ 3K/ngày, trải nghiệm cấu hình mạnh mẽ với phần cứng chuyên dụng AMD EPYC Gen 3, SSD NVMe U.2, băng thông cao cho tốc độ và sự ổn định vượt trội.
Khi nào nên và không nên dùng Đệ quy?
Sau khi đã tìm hiểu về cách hoạt động, ưu và nhược điểm, câu hỏi thực tế đặt ra là: “Khi nào tôi nên chọn đệ quy, và khi nào nên chọn vòng lặp?”. Không có câu trả lời tuyệt đối, nhưng đây là một số hướng dẫn dựa trên kinh nghiệm và các yếu tố đã phân tích.
Nên cân nhắc sử dụng Đệ quy khi:
- Bài toán có bản chất đệ quy tự nhiên: Đây là trường hợp lý tưởng nhất. Các cấu trúc dữ liệu như cây (duyệt cây), đồ thị (tìm kiếm theo chiều sâu – DFS), hoặc các bài toán có thể định nghĩa dựa trên chính nó (Giai thừa, Fibonacci – dù cần tối ưu) thường có lời giải đệ quy rất tự nhiên và dễ hiểu.
- Áp dụng các giải thuật Chia để trị (Divide and Conquer): Các thuật toán kinh điển như Mergesort, Quicksort, tìm kiếm nhị phân (Binary Search) vốn dựa trên việc chia bài toán thành các bài toán con giống hệt nhưng nhỏ hơn, rất phù hợp với cách tiếp cận đệ quy.
- Ưu tiên sự rõ ràng và ngắn gọn của code: Nếu một giải pháp đệ quy giúp mã nguồn trở nên sáng sủa, dễ đọc hơn đáng kể so với giải pháp vòng lặp phức tạp, và các yếu tố về hiệu suất, bộ nhớ không quá khắt khe, thì đệ quy là một lựa chọn tốt.
Nên tránh hoặc cẩn trọng khi sử dụng Đệ quy khi:
- Yêu cầu hiệu suất tối đa: Nếu ứng dụng đòi hỏi tốc độ xử lý cao nhất có thể, và có một giải pháp vòng lặp hiệu quả tương đương hoặc hơn, thì nên ưu tiên vòng lặp để tránh overhead của các lời gọi hàm.
- Độ sâu đệ quy có thể rất lớn: Nếu bạn dự đoán rằng số lần hàm tự gọi lại chính nó có thể lên tới hàng nghìn, hàng triệu lần (ví dụ: xử lý một danh sách rất dài một cách tuyến tính), nguy cơ Stack Overflow là rất cao. Lúc này, vòng lặp là lựa chọn an toàn hơn nhiều.
- Bài toán có thể giải quyết đơn giản bằng vòng lặp: Đừng cố gắng ép buộc sử dụng đệ quy cho những tác vụ lặp đơn giản mà một vòng
forhaywhilethông thường có thể xử lý một cách gọn gàng và hiệu quả. Hãy chọn công cụ phù hợp nhất và đơn giản nhất.
Cuối cùng, việc lựa chọn giữa đệ quy và vòng lặp là một sự cân nhắc giữa sự thanh lịch, rõ ràng của code và các yếu tố thực tế về hiệu suất, bộ nhớ. Kinh nghiệm thực tế sẽ giúp bạn đưa ra quyết định tốt hơn trong từng tình huống cụ thể.
Câu hỏi thường gặp về Đệ quy (FAQ)
Dưới đây là một số câu hỏi phổ biến mà những người mới học lập trình thường gặp khi tìm hiểu về đệ quy:
Đệ quy có khó học không?
Đệ quy có thể hơi khó nắm bắt ban đầu vì nó đòi hỏi một cách tư duy khác biệt so với vòng lặp tuần tự. Khái niệm một hàm tự gọi lại chính nó có vẻ hơi lạ. Tuy nhiên, chìa khóa nằm ở việc hiểu rõ hai thành phần: Trường hợp cơ sở (Base Case) và Bước đệ quy (Recursive Step), cùng với cách Call Stack hoạt động. Bắt đầu với các ví dụ đơn giản như giai thừa, Fibonacci và thực hành nhiều sẽ giúp bạn quen dần và thấy nó trở nên dễ dàng hơn.
Làm thế nào để tránh lỗi Stack Overflow?
Cách quan trọng nhất là đảm bảo hàm đệ quy của bạn luôn luôn có một hoặc nhiều Trường hợp cơ sở (Base Case) được định nghĩa chính xác và luôn luôn có thể đạt được sau một số hữu hạn các bước đệ quy. Hãy kiểm tra kỹ logic để chắc chắn rằng Bước đệ quy (Recursive Step) thực sự làm cho đầu vào tiến gần đến Base Case.
Nếu bài toán đòi hỏi độ sâu đệ quy quá lớn mà bạn không thể tránh được, hãy cân nhắc chuyển đổi thuật toán sang dạng vòng lặp (iteration). Đôi khi, việc sử dụng một cấu trúc dữ liệu stack tường minh trong code vòng lặp có thể mô phỏng lại hành vi của đệ quy mà không bị giới hạn bởi Call Stack của hệ thống.
Đệ quy đuôi (Tail Recursion) là gì?
Đệ quy đuôi (Tail Recursion) là một trường hợp đặc biệt của đệ quy, xảy ra khi lời gọi đệ quy là hành động cuối cùng được thực hiện trong hàm. Nghĩa là, sau khi lời gọi đệ quy trả về kết quả, hàm mẹ không cần thực hiện thêm bất kỳ phép tính nào khác mà chỉ cần trả về trực tiếp kết quả đó.
Điểm đặc biệt của đệ quy đuôi là nó có thể được tối ưu hóa bởi một số trình biên dịch hoặc trình thông dịch thông qua kỹ thuật gọi là Tối ưu hóa Đệ quy Đuôi (Tail Call Optimization – TCO). TCO cho phép tái sử dụng khung ngăn xếp (stack frame) hiện tại cho lời gọi đệ quy tiếp theo, thay vì tạo một khung mới.
Điều này giúp ngăn chặn việc Call Stack bị đầy lên, loại bỏ nguy cơ Stack Overflow và làm cho đệ quy đuôi hiệu quả về bộ nhớ tương tự như vòng lặp. Tuy nhiên, không phải tất cả các ngôn ngữ hoặc môi trường đều hỗ trợ TCO (ví dụ: CPython – trình thông dịch Python phổ biến nhất – không hỗ trợ TCO).











