Cây Nhị Phân Là Gì? (Binary Tree) – Đặc Điểm & Ví Dụ Dễ Hiểu

Nếu bạn đang học cấu trúc dữ liệu và thuật toán, thì khái niệm cây nhị phân (binary tree) chắc chắn là chủ đề không thể bỏ qua. Với thiết kế đơn giản nhưng cực kỳ hiệu quả, cây nhị phân xuất hiện ở mọi nơi trong lập trình. Trong bài viết này, bạn sẽ được giải thích từ khái niệm cơ bản, các thành phần cấu thành cây, phân loại đến ứng dụng và ví dụ minh họa rõ ràng, dễ hiểu.

Cây nhị phân (Binary Tree) là gì?

Cây nhị phân (Binary Tree) là một cấu trúc dữ liệu phân cấp, phi tuyến tính, được sử dụng rất phổ biến trong khoa học máy tính. Điểm đặc trưng nhất của nó là mỗi nút (node) trong cây chỉ có thể có tối đa hai nút con (child node).

Hai nút con này thường được phân biệt rõ ràng: một nút con trái (left child) và một nút con phải (right child). Chính giới hạn “tối đa hai con” này đã tạo nên tên gọi “nhị phân” (binary) cho cấu trúc dữ liệu này.

Hãy tưởng tượng cây nhị phân giống như một cây gia phả đơn giản, nơi mỗi người (nút) có tối đa hai người con. Cấu trúc này bắt đầu từ một nút gốc (root node) duy nhất ở trên cùng và phân nhánh xuống dưới, tạo thành một hệ thống thứ bậc rõ ràng.

Các thành phần chính cấu tạo nên cây nhị phân là các nút (chứa thông tin) và các cạnh (edge – đường nối giữa các nút). Cạnh thể hiện mối quan hệ cha-con (parent-child), kết nối một nút cha với các nút con trực tiếp của nó.

Tại sao gọi là “Nhị phân”?

Tên gọi “nhị phân” bắt nguồn trực tiếp từ đặc tính cơ bản nhất của cấu trúc này. Trong tiếng Latinh, “bi” có nghĩa là hai. Do đó, “nhị phân” ám chỉ rằng mỗi thành phần (mỗi nút) trong cây bị giới hạn ở việc có tối đa hai nhánh con trực tiếp đi xuống.

Điều này phân biệt cây nhị phân với các cấu trúc cây tổng quát hơn, nơi một nút có thể có nhiều hơn hai nút con. Ví dụ, khi bạn xem cấu trúc thư mục trên máy tính, một thư mục (nút cha) có thể chứa nhiều thư mục con hoặc tệp tin (nút con).

Giới hạn hai con này mang lại sự đơn giản trong việc quản lý và biểu diễn dữ liệu. Nó cũng là nền tảng cho nhiều thuật toán hiệu quả, đặc biệt là trong việc tìm kiếm và sắp xếp dữ liệu khi áp dụng các ràng buộc cụ thể (như trong Cây Nhị Phân Tìm Kiếm).

Vì vậy, khi nghe đến “cây nhị phân”, hãy nhớ ngay đến đặc điểm cốt lõi: mỗi nút có không quá hai con – một bên trái và một bên phải. Đây là chìa khóa để hiểu và làm việc với cấu trúc dữ liệu quan trọng này.

Các thuật ngữ quan trọng cần biết về Cây Nhị Phân

Để hiểu sâu hơn về cây nhị phân, chúng ta cần nắm vững một số thuật ngữ cơ bản. Việc này giống như học bảng chữ cái trước khi đọc một cuốn sách vậy. Đừng lo, các khái niệm này khá trực quan và dễ hiểu.

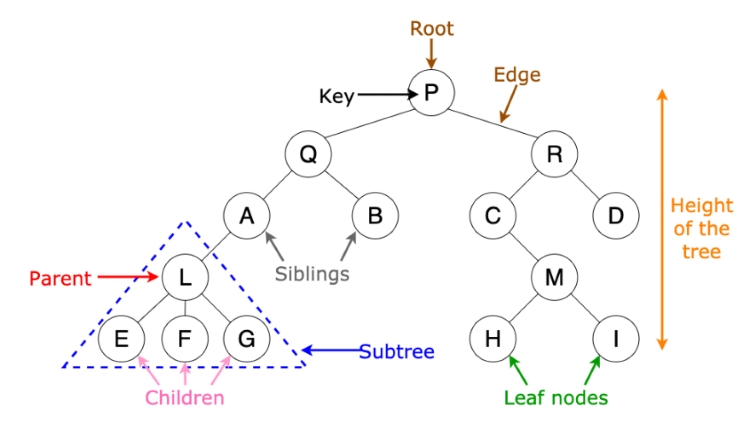
Nút (Node)

Nút là thành phần cơ bản nhất, đơn vị cấu tạo nên cây nhị phân. Mỗi nút thường chứa một giá trị dữ liệu nào đó (ví dụ: một con số, một ký tự, một đối tượng) và các liên kết (con trỏ hoặc tham chiếu) đến các nút con của nó (nếu có).

Hãy hình dung mỗi nút như một chiếc hộp. Bên trong hộp chứa dữ liệu, và từ hộp đó có thể có tối đa hai sợi dây nối đến hai chiếc hộp khác ở tầng dưới – đó là các nút con trái và con phải.

Trong nhiều ngôn ngữ lập trình như C++, Java, hay Python, một nút thường được biểu diễn bằng một lớp (class) hoặc cấu trúc (struct). Nó bao gồm một trường để lưu dữ liệu và hai trường con trỏ/tham chiếu left và right để chỉ đến các nút con tương ứng.

Python

# Ví dụ cấu trúc Nút đơn giản trong Python
class Node:
    def __init__(self, data):
        self.data = data  # Chứa dữ liệu của nút
        self.left = None  # Tham chiếu đến nút con trái, ban đầu là None
        self.right = None # Tham chiếu đến nút con phải, ban đầu là None

Đoạn mã trên minh họa một cách đơn giản cấu trúc của một nút. Mỗi khi tạo một nút mới, bạn cung cấp dữ liệu cho nó, và ban đầu, nó chưa có con nào (left và right đều là None).

Cạnh (Edge)

Cạnh là đường nối trực tiếp giữa hai nút trong cây, thể hiện mối quan hệ cha-con. Cụ thể, một cạnh sẽ nối từ một nút cha (parent node) đến một nút con (child node) của nó.

Trong các mô hình cây, cạnh thường được vẽ dưới dạng một đoạn thẳng nối hai nút. Nó biểu thị một liên kết hoặc một con trỏ từ nút cha đến nút con. Số lượng cạnh trong một cây luôn ít hơn số lượng nút đúng một đơn vị (Số cạnh = Số nút – 1).

Ví dụ, nếu nút A là cha của nút B, thì sẽ có một cạnh nối từ A xuống B. Cạnh này cho thấy B là hậu duệ trực tiếp của A. Các cạnh giúp xác định cấu trúc phân cấp và đường đi trong cây.

Nút Gốc (Root Node)

Nút gốc là nút đặc biệt nhất trong cây nhị phân. Đây là nút nằm ở vị trí cao nhất, là điểm khởi đầu của cây và không có nút cha nào. Mỗi cây nhị phân (nếu không rỗng) chỉ có duy nhất một nút gốc.

Hãy tưởng tượng nút gốc như gốc của một cái cây thật trong tự nhiên, từ đó mọi cành nhánh khác phát triển ra. Tất cả các nút khác trong cây đều là hậu duệ (con, cháu, chắt…) của nút gốc.

Nếu một cây nhị phân chỉ có đúng một nút, thì nút đó vừa là nút gốc, vừa là nút lá. Việc xác định nút gốc là bước đầu tiên trong hầu hết các thao tác xử lý trên cây, chẳng hạn như duyệt cây (tree traversal).

Nút Lá (Leaf Node)

Nút lá là những nút nằm ở vị trí “tận cùng” của các nhánh cây. Đặc điểm nhận dạng của nút lá là chúng không có bất kỳ nút con nào (cả con trái và con phải đều là None hoặc NULL).

Trong sơ đồ cây, các nút lá thường nằm ở tầng thấp nhất. Chúng đại diện cho điểm kết thúc của các đường đi từ nút gốc. Một cây nhị phân có thể có một hoặc nhiều nút lá.

Ví dụ, trong cây gia phả, những người không có con cái sẽ tương ứng với các nút lá. Việc xác định các nút lá rất quan trọng trong nhiều thuật toán, ví dụ như tính toán chiều cao của cây.

Nút Cha (Parent Node) & Nút Con (Child Node)

Mối quan hệ cha-con là cốt lõi của cấu trúc phân cấp trong cây nhị phân. Một nút cha là nút có các cạnh nối trực tiếp xuống các nút khác. Những nút được nối tới đó được gọi là nút con của nó.

Như đã đề cập, trong cây nhị phân, mỗi nút cha có thể có tối đa hai nút con: một nút con trái và một nút con phải. Ngược lại, mỗi nút (trừ nút gốc) chỉ có duy nhất một nút cha.

Mối quan hệ này tạo ra một cấu trúc thứ bậc rõ ràng. Nút A là cha của nút B nếu có một cạnh nối trực tiếp từ A đến B. Ngược lại, B là con của A. Hiểu rõ mối quan hệ này giúp chúng ta di chuyển và thao tác trên cây.

Nút Trung Gian (Internal Node)

Nút trung gian là bất kỳ nút nào trong cây mà không phải là nút lá. Điều này có nghĩa là một nút trung gian phải có ít nhất một nút con (con trái, con phải, hoặc cả hai).

Nút gốc cũng được xem là một nút trung gian nếu nó có ít nhất một nút con (tức là cây có nhiều hơn một nút). Các nút trung gian đóng vai trò kết nối, phân nhánh trong cấu trúc cây.

Tóm lại, các nút trong cây nhị phân có thể được phân loại thành: nút gốc, nút trung gian (không phải gốc và không phải lá), và nút lá. Tổng số nút trong cây bằng tổng số nút của ba loại này.

Cây con (Subtree)

Một cây con của một cây nhị phân là một nút trong cây đó cùng với tất cả các hậu duệ của nó (con, cháu, chắt…). Bản thân cây con cũng là một cây nhị phân hoàn chỉnh.

Mỗi nút trong cây nhị phân (trừ các nút lá) là gốc của hai cây con tiềm năng: cây con trái và cây con phải. Cây con trái bao gồm nút con trái và tất cả hậu duệ của nó. Tương tự với cây con phải.

Khái niệm cây con rất quan trọng vì nó thể hiện tính chất đệ quy của cây nhị phân. Nhiều thuật toán xử lý cây hoạt động dựa trên nguyên tắc giải quyết bài toán trên các cây con rồi kết hợp kết quả lại.

Độ sâu của Nút (Depth of a Node)

Độ sâu của một nút được định nghĩa là độ dài đường đi (số lượng cạnh) từ nút gốc đến nút đó. Theo quy ước, độ sâu của nút gốc là 0.

Các nút con trực tiếp của nút gốc sẽ có độ sâu là 1. Các nút con của những nút có độ sâu 1 sẽ có độ sâu là 2, và cứ thế tiếp tục. Độ sâu cho biết “mức” (level) của một nút trong cây.

Ví dụ, nếu đường đi từ gốc A đến nút D là A -> B -> D, thì đường đi này có 2 cạnh (A->B và B->D). Do đó, độ sâu của nút D là 2. Khái niệm này hữu ích khi phân tích cấu trúc theo từng tầng của cây.

Chiều cao của Cây (Height of a Tree)

Chiều cao của một cây nhị phân được định nghĩa là độ sâu lớn nhất của một nút lá trong cây đó. Nói cách khác, đó là độ dài đường đi dài nhất (tính bằng số cạnh) từ nút gốc đến một nút lá bất kỳ.

Theo một quy ước khác (đôi khi dùng số nút thay vì số cạnh), chiều cao có thể được tính bằng số nút trên đường đi dài nhất từ gốc đến lá. Nếu tính theo số cạnh, chiều cao của cây chỉ có một nút (gốc) là 0. Nếu tính theo số nút, chiều cao là 1. Chúng ta thường dùng định nghĩa theo số cạnh.

Chiều cao cho biết “độ vươn xa” của cây từ gốc. Ví dụ, nếu đường đi dài nhất từ gốc đến lá có 3 cạnh, thì chiều cao của cây là 3. Chiều cao là một thông số quan trọng để đánh giá hiệu suất của các thuật toán trên cây, đặc biệt là cây nhị phân tìm kiếm.

Bậc của Nút (Degree of a Node)

Bậc của một nút đơn giản là số lượng nút con mà nút đó có. Trong cây nhị phân, bậc của một nút chỉ có thể là 0, 1 hoặc 2.

• Bậc 0: Nút không có con nào (đây là nút lá).
• Bậc 1: Nút chỉ có một con (hoặc con trái, hoặc con phải).
• Bậc 2: Nút có đủ cả hai con (con trái và con phải).

Bậc của một nút cho biết khả năng phân nhánh tại nút đó. Khái niệm này giúp phân loại các nút trong cây (ví dụ: nút lá có bậc 0, nút đầy đủ có bậc 2).

Đặc điểm và tính chất cơ bản của Cây Nhị Phân

Sau khi nắm vững các thuật ngữ, chúng ta cùng tổng kết lại một số đặc điểm và tính chất quan trọng của cây nhị phân:

1. Cấu trúc phân cấp (Hierarchical Structure): Dữ liệu được tổ chức theo các mức, bắt đầu từ nút gốc, thể hiện mối quan hệ cha-con rõ ràng. Đây là cấu trúc phi tuyến tính, khác với mảng hay danh sách liên kết.
2. Giới hạn hai con: Mỗi nút có tối đa hai nút con, được gọi là con trái và con phải. Đây là đặc điểm định danh của cây nhị phân.
3. Thứ tự con (Optional): Trong cây nhị phân nói chung, thứ tự của con trái và con phải là quan trọng. Cây có nút A là gốc, B là con trái khác với cây có A là gốc, B là con phải. Tuy nhiên, trong một số ứng dụng cụ thể như Cây Nhị Phân Tìm Kiếm, thứ tự này còn mang thêm ý nghĩa về giá trị dữ liệu.
4. Tính đệ quy (Recursive Nature): Mỗi cây con (trái hoặc phải) của một nút trong cây nhị phân cũng chính là một cây nhị phân. Tính chất này cho phép áp dụng các giải thuật đệ quy một cách tự nhiên và hiệu quả.
5. Mối quan hệ giữa Số nút và Chiều cao: Chiều cao (h) của cây nhị phân có N nút nằm trong khoảng: floor(log2(N)) <= h <= N-1. Chiều cao tối thiểu đạt được ở cây gần hoàn chỉnh, và chiều cao tối đa xảy ra ở cây suy biến (giống danh sách liên kết).
6. Số nút tối đa ở một mức: Số lượng nút tối đa ở mức k (với gốc ở mức 0) là 2k. Điều này có nghĩa là số lượng nút tăng gấp đôi ở mỗi mức tiếp theo trong trường hợp cây “đầy” nhất có thể.
7. Tổng số nút tối đa: Một cây nhị phân có chiều cao h (tính theo số cạnh, gốc có chiều cao 0) có thể chứa tối đa 2h+1−1 nút. Điều này xảy ra khi cây là một cây nhị phân đầy đủ và tất cả các mức đều được lấp đầy.

Những đặc điểm và tính chất này làm cho cây nhị phân trở thành một công cụ mạnh mẽ và linh hoạt để biểu diễn dữ liệu và thiết kế các thuật toán hiệu quả trong nhiều lĩnh vực của khoa học máy tính.

Ví dụ minh họa về Cây Nhị Phân đơn giản

Lý thuyết sẽ dễ hiểu hơn rất nhiều khi có ví dụ thực tế. Hãy cùng xem xét một cây nhị phân đơn giản sau đây. Giả sử chúng ta có các nút chứa các giá trị số nguyên:

      10 (Gốc)
     /  \
    5    15
   / \    \
  3   7    20 (Lá)
 /       /
1 (Lá)  18 (Lá)

Hãy cùng phân tích cây này dựa trên các thuật ngữ đã học:

• Nút Gốc: Nút có giá trị 10.
• Các Nút: 10, 5, 15, 3, 7, 20, 1, 18. Tổng cộng có 8 nút.
• Các Cạnh: Có 7 cạnh nối các nút (10-5, 10-15, 5-3, 5-7, 15-20, 3-1, 20-18).
• Nút Cha & Nút Con:
  • 10 là cha của 5 và 15. 5 và 15 là con của 10.
  • 5 là cha của 3 và 7. 3 và 7 là con của 5.
  • 15 là cha của 20. 20 là con của 15 (con phải, không có con trái).
  • 3 là cha của 1. 1 là con của 3 (con trái, không có con phải).
  • 20 là cha của 18. 18 là con của 20 (con trái, không có con phải).
• Nút Lá: Các nút không có con: 7, 1, 18.
• Nút Trung Gian: Các nút có ít nhất một con: 10, 5, 15, 3, 20.
• Cây Con:
  • Nút 5 là gốc của cây con trái của nút 10 (gồm các nút 5, 3, 7, 1).
  • Nút 15 là gốc của cây con phải của nút 10 (gồm các nút 15, 20, 18).
• Độ Sâu:
  • Độ sâu của 10 (gốc) là 0.
  • Độ sâu của 5, 15 là 1.
  • Độ sâu của 3, 7, 20 là 2.
  • Độ sâu của 1, 18 là 3.
• Chiều Cao: Đường đi dài nhất từ gốc đến lá là 10 -> 15 -> 20 -> 18 (hoặc 10 -> 5 -> 3 -> 1), có 3 cạnh. Vậy chiều cao của cây này là 3.
• Bậc của Nút:
  • Bậc 2: 10, 5.
  • Bậc 1: 15, 3, 20.
  • Bậc 0: 7, 1, 18 (các nút lá).

Ví dụ này cho thấy cách các khái niệm liên kết với nhau trong một cấu trúc cây cụ thể. Bạn có thể thử vẽ lại cây này ra giấy để hình dung rõ hơn mối quan hệ giữa các nút.

Giới thiệu một số loại Cây Nhị Phân phổ biến

Cây nhị phân là một khái niệm tổng quát. Trên thực tế, có nhiều loại cây nhị phân đặc biệt được định nghĩa dựa trên các ràng buộc hoặc tính chất bổ sung. Hiểu về chúng giúp mở rộng kiến thức và ứng dụng của bạn. Dưới đây là giới thiệu sơ lược về ba loại phổ biến:

Cây Nhị Phân Tìm Kiếm (Binary Search Tree – BST)

Đây là loại cây nhị phân đặc biệt và cực kỳ quan trọng. Cây nhị phân tìm kiếm (BST) có thêm một ràng buộc chặt chẽ về giá trị dữ liệu lưu trữ trong các nút:

• Với mọi nút trong cây, tất cả các giá trị trong cây con trái của nó phải nhỏ hơn giá trị của nút đó.
• Tất cả các giá trị trong cây con phải của nó phải lớn hơn (hoặc bằng, tùy quy ước) giá trị của nút đó.

Đặc điểm này giúp việc tìm kiếm, thêm, xóa phần tử trong cây trở nên rất hiệu quả (trung bình là O(log N) với cây cân bằng). BST là nền tảng cho nhiều cấu trúc dữ liệu và thuật toán khác.

Ví dụ cây ở phần trước không phải là BST vì ví dụ, nút 18 (trong cây con phải của 15) lại nhỏ hơn 20 (cha trực tiếp). Một ví dụ về BST:

      8
     / \
    3   10
   / \    \
  1   6    14
     / \  /
    4   7 13

Bạn có thể kiểm tra thấy mọi nút đều tuân thủ quy tắc giá trị của BST.

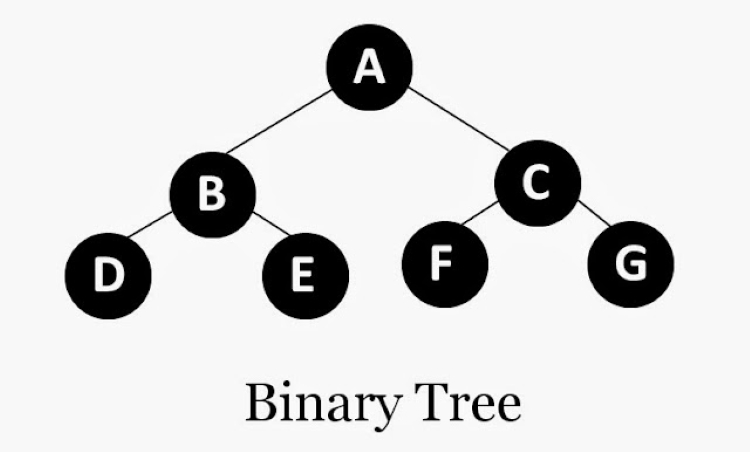
Cây Nhị Phân Đầy Đủ (Full Binary Tree)

Cây nhị phân đầy đủ (còn gọi là Proper Binary Tree) là cây mà mỗi nút trong đó chỉ có thể có 0 hoặc 2 nút con. Không có nút nào được phép chỉ có 1 nút con.

Nói cách khác, mọi nút trong cây nhị phân đầy đủ hoặc là nút lá (0 con) hoặc là nút trung gian có đủ cả hai con (trái và phải).

Ví dụ về cây đầy đủ:

      A
     / \
    B   C
       / \
      D   E

Trong cây này, A, C là nút có 2 con; B, D, E là nút lá (0 con). Không có nút nào chỉ có 1 con. Cây trong ví dụ minh họa đầu tiên không phải là cây đầy đủ (ví dụ nút 15, 3, 20 chỉ có 1 con).

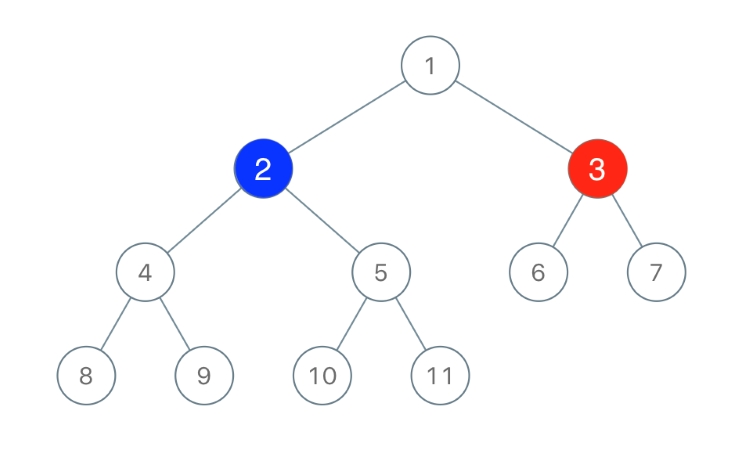
Cây Nhị Phân Hoàn Chỉnh (Complete Binary Tree)

Cây nhị phân hoàn chỉnh là loại cây có một định nghĩa hơi khác một chút. Một cây nhị phân được gọi là hoàn chỉnh nếu:

1. Tất cả các mức, ngoại trừ có thể là mức cuối cùng, đều được lấp đầy hoàn toàn.
2. Nếu mức cuối cùng chưa đầy, thì các nút ở mức này phải được điền từ trái sang phải.

Đặc điểm này làm cho cây nhị phân hoàn chỉnh rất phù hợp để biểu diễn bằng mảng một cách hiệu quả, đặc biệt trong cấu trúc dữ liệu Heap (đống).

Ví dụ về cây hoàn chỉnh:

      1
     / \
    2   3
   / \ /
  4  5 6

Cây này có chiều cao 2. Mức 0 (nút 1), mức 1 (nút 2, 3) đều đầy. Mức 2 (mức cuối) có nút 4, 5, 6 được điền từ trái sang phải. Nếu thêm nút 7, nó phải là con phải của nút 3.

Cần phân biệt rõ ràng giữa cây đầy đủ và cây hoàn chỉnh. Một cây có thể là đầy đủ nhưng không hoàn chỉnh, hoàn chỉnh nhưng không đầy đủ, vừa đầy đủ vừa hoàn chỉnh, hoặc không là cả hai.

Ứng dụng cơ bản của Cây Nhị Phân trong thực tế

Vậy câu hỏi đặt ra là, học cây nhị phân để làm gì? Cấu trúc dữ liệu này có vẻ trừu tượng, nhưng nó có rất nhiều ứng dụng quan trọng và là nền tảng trong lập trình:

1. Biểu diễn cấu trúc phân cấp: Cây nhị phân rất tự nhiên để mô tả các mối quan hệ phân cấp. Ví dụ như sơ đồ tổ chức công ty, hệ thống phân loại sinh học, hay cấu trúc DOM (Document Object Model) của một trang web HTML.
2. Cây Nhị Phân Tìm Kiếm (BST): Như đã đề cập, BST cho phép tìm kiếm, thêm, xóa dữ liệu rất nhanh chóng. Nó được dùng trong việc cài đặt các cấu trúc như tập hợp (Set) và ánh xạ (Map) trong nhiều thư viện chuẩn.
3. Cây biểu thức (Expression Trees): Cây nhị phân có thể dùng để biểu diễn các biểu thức toán học. Các toán tử (+, -, *, /) là các nút trung gian, còn các toán hạng (số) là các nút lá. Việc duyệt cây theo các thứ tự khác nhau (inorder, preorder, postorder) sẽ cho ra các dạng biểu diễn khác nhau của biểu thức (trung tố, tiền tố, hậu tố).
4. Cấu trúc Heap (Đống): Heap là một cấu trúc dữ liệu dựa trên cây nhị phân hoàn chỉnh, thường được dùng để cài đặt hàng đợi ưu tiên (Priority Queue). Heap rất hiệu quả trong việc tìm phần tử lớn nhất/nhỏ nhất.
5. Thuật toán nén dữ liệu: Các thuật toán nén như Huffman Coding sử dụng cây nhị phân để xây dựng mã tối ưu cho các ký tự dựa trên tần suất xuất hiện của chúng, giúp giảm kích thước dữ liệu hiệu quả.
6. Cây quyết định (Decision Trees): Trong lĩnh vực học máy (Machine Learning), cây quyết định là một mô hình dự đoán sử dụng cấu trúc cây (thường là cây nhị phân) để đưa ra quyết định dựa trên các đặc trưng của dữ liệu.

Những ứng dụng này cho thấy tầm quan trọng của việc nắm vững khái niệm cây nhị phân. Nó không chỉ là lý thuyết suông mà còn là công cụ mạnh mẽ được áp dụng trong nhiều bài toán thực tế.

Những nhầm lẫn thường gặp khi học Cây Nhị Phân

Khi mới tiếp cận cây nhị phân, người học thường gặp một số điểm dễ gây nhầm lẫn. Hiểu rõ những điều này sẽ giúp bạn tránh được các sai sót không đáng có:

1. Nhầm lẫn Chiều cao và Độ sâu: Độ sâu là thuộc tính của từng nút (khoảng cách từ gốc đến nút đó), trong khi Chiều cao là thuộc tính của toàn bộ cây (độ sâu lớn nhất của nút lá). Chiều cao của cây bằng chiều cao của nút gốc.
2. Cây Nhị Phân vs. Cây Nhị Phân Tìm Kiếm (BST): Không phải mọi cây nhị phân đều là BST. BST là một trường hợp đặc biệt của cây nhị phân có thêm ràng buộc về giá trị nút. Cần kiểm tra điều kiện giá trị mới kết luận một cây là BST.
3. Cây Đầy đủ vs. Cây Hoàn chỉnh: Hai khái niệm này khác nhau. Cây đầy đủ yêu cầu mọi nút phải có 0 hoặc 2 con. Cây hoàn chỉnh yêu cầu các mức phải đầy từ trái sang, trừ mức cuối cùng. Hãy xem lại định nghĩa và ví dụ để phân biệt rõ.
4. Thứ tự con: Trong cây nhị phân, việc một nút là con trái hay con phải rất quan trọng và tạo ra các cây khác nhau về mặt cấu trúc, ngay cả khi chúng chứa cùng một tập hợp các nút.
5. Biểu diễn bằng mảng: Chỉ có cây nhị phân hoàn chỉnh mới thực sự phù hợp để biểu diễn hiệu quả bằng mảng. Việc cố gắng biểu diễn cây không hoàn chỉnh bằng mảng có thể gây lãng phí bộ nhớ lớn.

Nhận biết và tránh được những nhầm lẫn này sẽ giúp bạn xây dựng nền tảng kiến thức vững chắc hơn về cấu trúc dữ liệu quan trọng này.