Stack (Ngăn xếp) là gì? CTDL Stack, Nguyên tắc LIFO & Ví dụ

Trong khoa học máy tính và lập trình, việc hiểu và sử dụng hiệu quả các cấu trúc dữ liệu và giải thuật là nền tảng cốt lõi. Một trong những cấu trúc dữ liệu cơ bản nhưng cực kỳ quan trọng đó chính là Stack (Ngăn xếp). Dù bạn là sinh viên mới bắt đầu hay lập trình viên đang tìm cách tối ưu code, nắm vững về Stack là điều cần thiết.

Bài viết này sẽ đi sâu giải thích Stack là gì, nguyên tắc hoạt động LIFO đặc trưng, các thao tác cơ bản, cách triển khai phổ biến, những ứng dụng thực tế quan trọng và cả những lỗi thường gặp. Hãy cùng khám phá cấu trúc dữ liệu thú vị này nhé!

Stack (ngăn xếp) là gì?

Stack (hay ngăn xếp) là một cấu trúc dữ liệu tuyến tính cơ bản trong khoa học máy tính. Nó hoạt động theo nguyên tắc LIFO (Last-In, First-Out), nghĩa là phần tử nào được thêm vào (push) sau cùng sẽ là phần tử đầu tiên được truy cập hoặc lấy ra (pop). Stack lưu trữ một tập hợp các phần tử (elements) theo một trật tự nhất định.

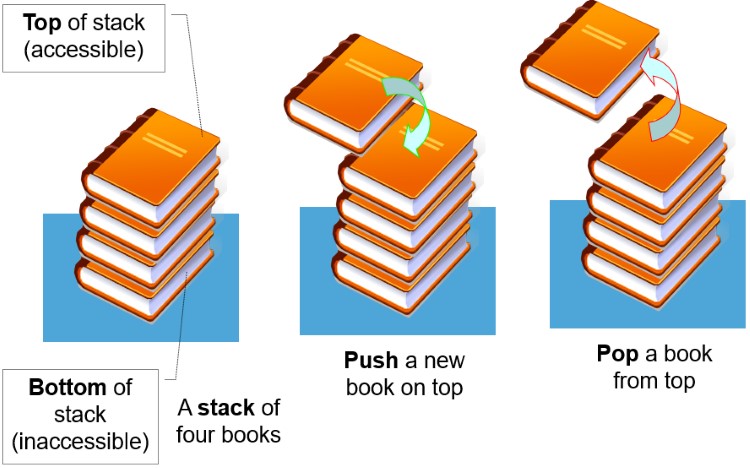
“Tuyến tính” ở đây có nghĩa là các phần tử được tổ chức theo một chuỗi tuần tự, phần tử này nối tiếp phần tử kia. Bạn có thể hình dung nó như một con đường thẳng, nơi bạn chỉ có thể thêm hoặc bớt các phần tử ở một đầu duy nhất, được gọi là đỉnh (top) của stack.

Khái niệm stack rất trực quan và dễ hình dung thông qua các ví dụ đời thường. Điều này giúp người mới bắt đầu dễ dàng tiếp cận và hiểu được bản chất của cấu trúc dữ liệu này trước khi đi sâu vào các khía cạnh kỹ thuật phức tạp hơn.

Ví dụ minh họa dễ hiểu: Chồng đĩa và nguyên tắc LIFO

Hãy tưởng tượng một chồng đĩa ăn sạch được xếp chồng lên nhau gọn gàng trên bàn. Khi bạn rửa xong một chiếc đĩa mới, bạn sẽ đặt nó lên trên cùng của chồng đĩa. Đây chính là hành động tương tự như thao tác Push trong Stack – thêm một phần tử mới vào đỉnh.

Ngược lại, khi bạn cần lấy một chiếc đĩa để sử dụng, bạn cũng phải lấy chiếc đĩa đang nằm ở trên cùng ra trước tiên. Bạn không thể rút một chiếc đĩa ở giữa chồng đĩa ra mà không làm đổ cả chồng. Hành động này tương ứng với thao tác Pop – lấy phần tử trên cùng ra khỏi Stack.

Ví dụ đơn giản này minh họa hoàn hảo nguyên tắc LIFO (Last-In, First-Out). Chiếc đĩa bạn đặt lên sau cùng (Last-In) chính là chiếc đĩa bạn phải lấy ra đầu tiên (First-Out). Stack trong lập trình hoạt động chính xác theo logic này.

Một ví dụ khác cũng rất quen thuộc là nút “Back” trên trình duyệt web. Mỗi khi bạn truy cập một trang mới, địa chỉ trang đó được “đẩy” (push) vào một stack lịch sử. Khi bạn nhấn nút “Back”, trang cuối cùng bạn truy cập (last-in) sẽ được “lấy ra” (pop) và hiển thị (first-out).

Nguyên tắc LIFO (Last-In, First-Out) hoạt động như thế nào?

LIFO (Last-In, First-Out) là nguyên tắc vận hành cốt lõi và định nghĩa nên cấu trúc dữ liệu Stack. Nó mô tả thứ tự mà các phần tử được thêm vào và lấy ra khỏi stack. Hiểu rõ LIFO là chìa khóa để sử dụng stack một cách chính xác trong các thuật toán và ứng dụng.

Giải thích chi tiết “Vào sau – Ra trước”

Cụm từ “Vào sau – Ra trước” (Last-In, First-Out) có nghĩa là phần tử dữ liệu được thêm vào stack gần đây nhất (sau cùng) sẽ là phần tử đầu tiên được phép lấy ra hoặc xử lý. Giống như chồng đĩa, bạn chỉ có thể tương tác với phần tử ở trên cùng (top) của stack.

Khi một phần tử mới được thêm vào (Push), nó sẽ chiếm vị trí trên cùng. Khi một phần tử được lấy ra (Pop), chính phần tử ở trên cùng đó sẽ bị loại bỏ, và phần tử nằm ngay dưới nó (nếu có) sẽ trở thành đỉnh mới của stack.

Nguyên tắc LIFO này làm cho Stack trở nên lý tưởng cho các tác vụ cần đảo ngược thứ tự, quản lý các trạng thái lồng nhau (như lời gọi hàm), hoặc thực hiện các thao tác quay lui (backtracking) trong thuật toán.

Điều này hoàn toàn trái ngược với cấu trúc dữ liệu Queue (Hàng đợi), vốn hoạt động theo nguyên tắc FIFO (First-In, First-Out) – “Vào trước, Ra trước”. Trong Queue, phần tử được thêm vào đầu tiên sẽ là phần tử được xử lý đầu tiên, giống như hàng người xếp hàng chờ đợi.

Các thao tác (Operations) cơ bản trên Stack

Để tương tác và quản lý dữ liệu trong Stack, chúng ta sử dụng một tập hợp các thao tác (operations) cơ bản. Những thao tác này định nghĩa “giao diện” của Stack, cho phép chúng ta thêm, bớt, hoặc kiểm tra các phần tử một cách nhất quán theo nguyên tắc LIFO.

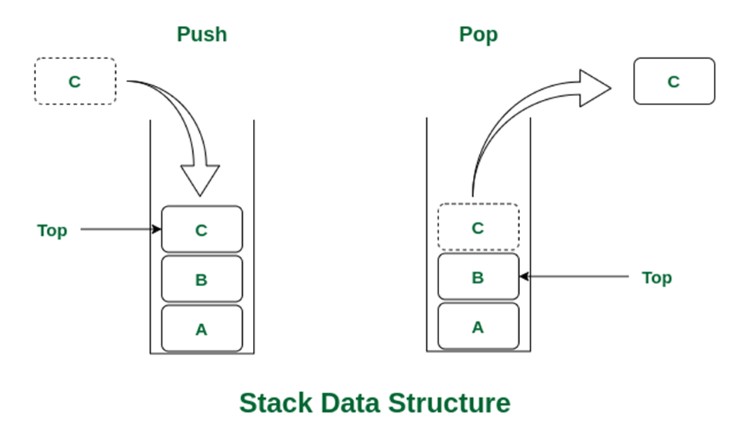
1. Push: Thêm phần tử vào đỉnh Stack

Thao tác Push được sử dụng để thêm một phần tử mới vào vị trí trên cùng (top) của stack. Sau khi push, phần tử mới này sẽ trở thành đỉnh mới của stack. Kích thước của stack sẽ tăng lên 1 sau mỗi lần push thành công.

Ví dụ, nếu stack đang chứa [A, B] (với B là đỉnh), sau khi thực hiện Push(C), stack sẽ trở thành [A, B, C] (với C là đỉnh mới).

Trong trường hợp stack được cài đặt bằng mảng có kích thước cố định, thao tác Push có thể thất bại nếu stack đã đầy (trạng thái overflow). Cần kiểm tra trạng thái isFull (nếu có) trước khi thực hiện Push.

// Giả mã cho thao tác Push
PROCEDURE Push(stack, element)
  IF IsFull(stack) THEN
    SIGNAL StackOverflowError
  ELSE
    stack.top = stack.top + 1
    stack.data[stack.top] = element
  ENDIF
ENDPROCEDURE

2. Pop: Lấy và xóa phần tử khỏi đỉnh Stack

Thao tác Pop được sử dụng để lấy ra và đồng thời xóa bỏ phần tử đang ở vị trí trên cùng (top) của stack. Phần tử nằm ngay dưới (nếu có) sẽ trở thành đỉnh mới. Kích thước của stack sẽ giảm đi 1 sau mỗi lần pop thành công.

Ví dụ, nếu stack đang là [A, B, C] (C là đỉnh), sau khi thực hiện Pop(), stack sẽ trở thành [A, B] (B là đỉnh mới) và giá trị C sẽ được trả về.

Nếu cố gắng thực hiện Pop trên một stack rỗng, lỗi Stack Underflow sẽ xảy ra. Do đó, cần kiểm tra trạng thái isEmpty trước khi thực hiện Pop để tránh lỗi này.

// Giả mã cho thao tác Pop
FUNCTION Pop(stack) : ElementType
  IF IsEmpty(stack) THEN
    SIGNAL StackUnderflowError
  ELSE
    element = stack.data[stack.top]
    stack.top = stack.top - 1
    RETURN element
  ENDIF
ENDFUNCTION

3. Peek (hoặc Top): Xem phần tử ở đỉnh Stack (không xóa)

Thao tác Peek (đôi khi còn gọi là Top) cho phép chúng ta xem giá trị của phần tử đang ở đỉnh stack mà không xóa bỏ nó. Thao tác này rất hữu ích khi bạn cần biết phần tử tiếp theo sẽ được xử lý là gì mà không muốn thay đổi trạng thái hiện tại của stack.

Ví dụ, nếu stack là [A, B, C] (C là đỉnh), thực hiện Peek() sẽ trả về giá trị C, nhưng stack vẫn giữ nguyên là [A, B, C].

Tương tự như Pop, việc thực hiện Peek trên stack rỗng cũng sẽ gây lỗi. Cần kiểm tra isEmpty trước khi thực hiện Peek.

// Giả mã cho thao tác Peek
FUNCTION Peek(stack) : ElementType
  IF IsEmpty(stack) THEN
    SIGNAL StackEmptyError
  ELSE
    RETURN stack.data[stack.top]
  ENDIF
ENDFUNCTION

(Tùy chọn) Các thao tác khác: isEmpty, isFull, Size

Ngoài ba thao tác cốt lõi trên, Stack thường có thêm một số thao tác phụ trợ hữu ích:

• isEmpty(): Kiểm tra xem stack có rỗng hay không. Trả về true nếu rỗng, false nếu ngược lại. Thao tác này cực kỳ quan trọng để tránh lỗi Stack Underflow khi Pop hoặc Peek.
• isFull(): Kiểm tra xem stack có đầy hay không. Thao tác này chủ yếu liên quan đến stack cài đặt bằng mảng có kích thước cố định. Trả về true nếu đầy, false nếu còn chỗ. Quan trọng để tránh lỗi Stack Overflow khi Push.
• Size(): Trả về số lượng phần tử hiện có trong stack.

Các thao tác phụ trợ này giúp việc quản lý và sử dụng stack trở nên an toàn và hiệu quả hơn, đặc biệt là trong việc xử lý các trường hợp biên (edge cases).

Cách cài đặt Stack phổ biến (Stack Implementation)

Stack là một Kiểu dữ liệu trừu tượng (Abstract Data Type – ADT). Điều này có nghĩa là chúng ta định nghĩa Stack dựa trên hành vi của nó (nguyên tắc LIFO và các thao tác Push, Pop, Peek) chứ không phải cách nó được lưu trữ cụ thể trong bộ nhớ.

Tuy nhiên, để sử dụng Stack trong lập trình, chúng ta cần một cấu trúc dữ liệu cụ thể bên dưới để cài đặt (implement) nó. Có hai cách cài đặt Stack phổ biến nhất là sử dụng Mảng (Array) và Danh sách liên kết (Linked List).

Cài đặt Stack bằng mảng (Array-based Stack)

Đây là cách cài đặt đơn giản và thường gặp. Chúng ta sử dụng một mảng (thường là mảng một chiều) để lưu trữ các phần tử của stack. Cần thêm một biến, thường gọi là top, để theo dõi chỉ số (index) của phần tử nằm ở đỉnh stack.

• Khởi tạo: Tạo một mảng với kích thước cố định (maxSize) và khởi tạo top = -1 (biểu thị stack rỗng).
• Push(element): Tăng top lên 1, sau đó gán element vào array[top]. Cần kiểm tra isFull (khi top == maxSize - 1) trước khi thực hiện.
• Pop(): Lấy giá trị tại array[top], sau đó giảm top đi 1. Cần kiểm tra isEmpty (khi top == -1) trước.
• Peek(): Trả về giá trị tại array[top]. Cần kiểm tra isEmpty.

Ưu điểm và nhược điểm (Array-based)

• Ưu điểm:
  • Cài đặt tương đối đơn giản.
  • Truy cập phần tử nhanh chóng (O(1)) do tính chất truy cập trực tiếp của mảng.
  • Có thể hiệu quả hơn về bộ nhớ đệm (cache locality) do các phần tử nằm liền kề nhau.
• Nhược điểm:
  • Kích thước cố định: Phải xác định kích thước tối đa ngay từ đầu. Nếu không đủ lớn, sẽ xảy ra Stack Overflow. Nếu quá lớn, sẽ lãng phí bộ nhớ.
  • Việc thay đổi kích thước mảng (resizing) nếu cần là một thao tác tốn kém.

Cài đặt Stack bằng Danh sách liên kết (Linked List-based Stack)

Cách cài đặt này sử dụng cấu trúc Danh sách liên kết đơn (Singly Linked List). Mỗi phần tử của stack được lưu trữ trong một nút (node). Mỗi nút chứa dữ liệu của phần tử và một con trỏ (pointer) trỏ đến nút tiếp theo bên dưới nó trong stack. Biến top sẽ là một con trỏ trỏ đến nút ở đỉnh stack.

• Khởi tạo: top = NULL (biểu thị stack rỗng).
• Push(element): Tạo một nút mới chứa element. Cho con trỏ next của nút mới trỏ đến nút top hiện tại. Cập nhật top để trỏ đến nút mới này.
• Pop(): Lưu lại con trỏ đến nút top hiện tại (temp). Cập nhật top để trỏ đến top->next. Trả về dữ liệu của nút temp và giải phóng bộ nhớ của nút temp. Cần kiểm tra isEmpty (top == NULL).
• Peek(): Trả về dữ liệu của nút top. Cần kiểm tra isEmpty.

Ưu điểm và nhược điểm (Linked List-based)

• Ưu điểm:
  • Kích thước động: Stack có thể phát triển hoặc thu nhỏ tùy theo nhu cầu, không bị giới hạn kích thước cố định (chỉ giới hạn bởi bộ nhớ hệ thống). Không xảy ra Stack Overflow do hết dung lượng cài đặt.
  • Sử dụng bộ nhớ hiệu quả hơn khi số lượng phần tử thay đổi nhiều, không lãng phí bộ nhớ như mảng cố định.
• Nhược điểm:
  • Mỗi phần tử tốn thêm bộ nhớ để lưu con trỏ next.
  • Truy cập có thể chậm hơn một chút so với mảng do các nút không nằm liền kề trong bộ nhớ (cache locality kém hơn).
  • Cài đặt có thể phức tạp hơn một chút so với dùng mảng.

Lựa chọn cách cài đặt nào?

Việc lựa chọn giữa cài đặt bằng Mảng hay Danh sách liên kết phụ thuộc vào yêu cầu cụ thể của bài toán:

• Chọn Mảng khi: Bạn biết trước giới hạn số lượng phần tử tối đa, hoặc khi hiệu suất truy cập là ưu tiên hàng đầu và kích thước stack không thay đổi quá nhiều.
• Chọn Danh sách liên kết khi: Bạn không biết trước số lượng phần tử, cần sự linh hoạt về kích thước, hoặc muốn tránh nguy cơ Stack Overflow do giới hạn kích thước cố định.

Trong nhiều thư viện chuẩn của các ngôn ngữ lập trình, Stack thường được cài đặt dựa trên các cấu trúc dữ liệu động như danh sách liên kết hoặc mảng động (có khả năng tự thay đổi kích thước).

Ứng dụng thực tế quan trọng của Stack trong lập trình

Mặc dù là một cấu trúc dữ liệu đơn giản, Stack lại có mặt trong vô số ứng dụng quan trọng và nền tảng của ngành khoa học máy tính và phát triển phần mềm. Hiểu các ứng dụng này giúp chúng ta thấy rõ giá trị và sức mạnh của Stack.

Quản lý lời gọi hàm (Function Call Stack) & Đệ quy (Recursion)

Đây là một trong những ứng dụng nền tảng nhất của Stack. Khi một hàm được gọi trong chương trình, thông tin về lời gọi hàm đó (như địa chỉ trả về, các tham số, biến cục bộ) được đẩy (push) vào một vùng nhớ đặc biệt gọi là Call Stack (Ngăn xếp lời gọi hàm).

Khi hàm con được gọi từ bên trong hàm cha, thông tin của hàm con lại được push lên trên đỉnh Call Stack. Khi một hàm thực thi xong, thông tin của nó được lấy ra (pop) khỏi Call Stack, và chương trình quay trở lại thực thi tại địa chỉ trả về đã lưu.

Cơ chế này hoạt động hoàn hảo với Đệ quy (Recursion) – kỹ thuật một hàm tự gọi lại chính nó. Mỗi lần hàm tự gọi, một frame mới lại được push vào Call Stack. Stack giúp quản lý thứ tự thực thi và trạng thái của các lời gọi hàm lồng nhau này. Nếu đệ quy quá sâu, Call Stack có thể bị đầy, gây ra lỗi Stack Overflow.

Tính năng Hoàn tác/Làm lại (Undo/Redo)

Nhiều ứng dụng phần mềm (như trình soạn thảo văn bản, phần mềm đồ họa) cung cấp tính năng Undo/Redo. Stack là cấu trúc dữ liệu lý tưởng để cài đặt tính năng này.

Mỗi khi người dùng thực hiện một hành động (như gõ chữ, xóa, vẽ hình), trạng thái hoặc hành động đó có thể được push vào một “Undo Stack”. Khi người dùng nhấn Undo, hành động trên cùng của Undo Stack được pop ra, hành động được hoàn tác, và hành động đó có thể được push vào một “Redo Stack”.

Khi người dùng nhấn Redo, hành động trên cùng của Redo Stack được pop ra, hành động được thực hiện lại, và nó lại được push trở lại vào Undo Stack. Nguyên tắc LIFO đảm bảo các hành động được hoàn tác/làm lại theo đúng thứ tự ngược lại.

Kiểm tra tính hợp lệ của dấu ngoặc (Parentheses Matching)

Trong các ngôn ngữ lập trình hoặc biểu thức toán học, việc các cặp dấu ngoặc (như (), [], {}) được đặt đúng vị trí và khớp với nhau là rất quan trọng. Stack có thể được sử dụng hiệu quả để kiểm tra tính hợp lệ này.

Thuật toán hoạt động như sau: Duyệt qua biểu thức từ trái sang phải. Nếu gặp dấu ngoặc mở ((, [, {), push nó vào stack. Nếu gặp dấu ngoặc đóng (), ], }), kiểm tra xem stack có rỗng không. Nếu rỗng, biểu thức không hợp lệ. Nếu không rỗng, pop phần tử trên cùng ra và kiểm tra xem nó có phải là dấu ngoặc mở tương ứng không. Nếu không khớp, biểu thức không hợp lệ.

Sau khi duyệt hết biểu thức, nếu stack rỗng thì biểu thức hợp lệ, ngược lại là không hợp lệ. Ví dụ: {[()]}là hợp lệ, trong khi [{)] là không hợp lệ.

Duyệt đồ thị theo chiều sâu (DFS – Depth-First Search)

Depth-First Search (DFS) là một thuật toán duyệt hoặc tìm kiếm trên cấu trúc dữ liệu đồ thị (Graph) hoặc cây (Tree). Tư tưởng của DFS là đi sâu nhất có thể vào một nhánh trước khi quay lui (backtrack) và khám phá nhánh khác.

Stack là công cụ cốt lõi để cài đặt DFS một cách tường minh (iterative DFS). Thuật toán bắt đầu bằng cách push nút gốc (start node) vào stack. Chừng nào stack chưa rỗng, pop một nút ra, xử lý nó (ví dụ: đánh dấu đã thăm), sau đó push tất cả các nút hàng xóm chưa được thăm của nó vào stack. Thứ tự LIFO đảm bảo thuật toán luôn ưu tiên đi sâu hơn.

Đánh giá biểu thức (Infix to Postfix/Prefix Conversion & Evaluation)

Con người thường viết biểu thức toán học theo dạng Infix (toán tử nằm giữa toán hạng, ví dụ: a + b). Tuy nhiên, máy tính thường xử lý hiệu quả hơn với dạng Postfix (toán tử đi sau toán hạng, ví dụ: a b +) hoặc Prefix (toán tử đứng trước toán hạng, ví dụ: + a b).

Stack đóng vai trò quan trọng trong cả hai quá trình:

1. Chuyển đổi Infix sang Postfix/Prefix: Thuật toán Shunting-yard nổi tiếng sử dụng stack để tạm giữ các toán tử và dấu ngoặc trong quá trình quét biểu thức Infix, từ đó tạo ra biểu thức Postfix tương đương.
2. Đánh giá biểu thức Postfix/Prefix: Stack được dùng để lưu trữ các toán hạng. Khi gặp một toán hạng, push nó vào stack. Khi gặp một toán tử, pop đủ số lượng toán hạng cần thiết ra khỏi stack, thực hiện phép toán, rồi push kết quả trở lại stack. Kết quả cuối cùng sẽ là giá trị duy nhất còn lại trong stack.

Các ứng dụng khác…

Ngoài các ứng dụng nổi bật trên, Stack còn được sử dụng trong nhiều lĩnh vực khác như:

• Thuật toán quay lui (Backtracking): Lưu lại các trạng thái hoặc lựa chọn để có thể quay lại nếu đi vào ngõ cụt.
• Quản lý lịch sử trình duyệt: Nút “Back” hoạt động dựa trên stack.
• Quản lý bộ nhớ: Biến cục bộ của hàm thường được cấp phát trên Call Stack.
• Một số thuật toán sắp xếp hoặc xử lý dữ liệu khác.

So sánh Stack và Queue: Phân biệt LIFO và FIFO

Stack và Queue (Hàng đợi) là hai cấu trúc dữ liệu tuyến tính cơ bản và thường được nhắc đến cùng nhau. Mặc dù có một số điểm tương đồng, chúng khác biệt hoàn toàn về nguyên tắc hoạt động cốt lõi, dẫn đến các ứng dụng khác nhau. Việc phân biệt rõ ràng giữa chúng là rất quan trọng.

Điểm giống nhau

• Cấu trúc tuyến tính: Cả hai đều tổ chức dữ liệu theo một chuỗi tuần tự.
• Kiểu dữ liệu trừu tượng (ADT): Cả hai đều được định nghĩa bởi hành vi và các thao tác hơn là cách cài đặt cụ thể.
• Cách cài đặt: Cả Stack và Queue đều có thể được cài đặt bằng Mảng hoặc Danh sách liên kết.
• Thao tác cơ bản: Cả hai đều có thao tác để thêm phần tử và xóa phần tử.

Điểm khác biệt cốt lõi (LIFO vs FIFO)

Sự khác biệt căn bản nằm ở thứ tự truy cập và xóa phần tử:

• Stack: Hoạt động theo nguyên tắc LIFO (Last-In, First-Out). Phần tử được thêm vào sau cùng sẽ là phần tử được lấy ra đầu tiên. Giống như chồng đĩa. Thao tác thêm là Push, thao tác xóa là Pop. Chỉ có thể thao tác ở một đầu (đỉnh – top).
• Queue: Hoạt động theo nguyên tắc FIFO (First-In, First-Out). Phần tử được thêm vào đầu tiên sẽ là phần tử được lấy ra đầu tiên. Giống như hàng người xếp hàng. Thao tác thêm thường gọi là Enqueue (thêm vào cuối – rear), thao tác xóa là Dequeue (xóa ở đầu – front). Thao tác diễn ra ở hai đầu khác nhau.

Khi nào dùng Stack, khi nào dùng Queue?

Việc lựa chọn cấu trúc dữ liệu phù hợp phụ thuộc vào yêu cầu của bài toán về thứ tự xử lý dữ liệu:

• Sử dụng Stack khi:
  • Cần đảo ngược thứ tự của dữ liệu.
  • Cần xử lý các tác vụ lồng nhau hoặc đệ quy (lời gọi hàm, kiểm tra ngoặc).
  • Cần thực hiện quay lui (backtracking) trong thuật toán.
  • Cần mô hình hóa các hành động Undo/Redo.
• Sử dụng Queue khi:
  • Cần duy trì thứ tự ban đầu của dữ liệu (ai đến trước phục vụ trước).
  • Cần xử lý các tác vụ theo tuần tự đến (requests server, hàng đợi in ấn).
  • Cần thực hiện duyệt đồ thị theo chiều rộng (BFS – Breadth-First Search).
  • Mô hình hóa hàng đợi trong đời thực.

Hiểu rõ sự khác biệt LIFO và FIFO giúp lập trình viên lựa chọn đúng công cụ cho đúng vấn đề, dẫn đến code hiệu quả và logic hơn.

Lỗi thường gặp cần biết: Stack Overflow là gì?

Stack Overflow Error (Lỗi tràn bộ nhớ stack) là một lỗi runtime khá phổ biến, xảy ra khi một chương trình cố gắng sử dụng nhiều bộ nhớ trên Call Stack hơn dung lượng được cấp phát cho nó. Hiểu nguyên nhân và cách phòng tránh lỗi này là kỹ năng quan trọng.

Nguyên nhân gây ra lỗi Stack Overflow

Nguyên nhân chính thường liên quan đến việc Call Stack bị lấp đầy quá nhanh hoặc quá sâu:

1. Đệ quy quá sâu (Excessive Recursion): Đây là nguyên nhân phổ biến nhất. Nếu một hàm đệ quy tự gọi lại chính nó quá nhiều lần mà không đạt đến trường hợp cơ sở (base case) để dừng lại, mỗi lời gọi hàm sẽ push một frame mới vào Call Stack. Khi Call Stack hết chỗ, lỗi Stack Overflow xảy ra.
2. Đệ quy vô hạn (Infinite Recursion): Trường hợp hàm đệ quy không bao giờ đạt đến điều kiện dừng, dẫn đến việc push vô hạn vào Call Stack.
3. Biến cục bộ quá lớn: Khai báo các biến cục bộ (local variables) có kích thước rất lớn (ví dụ: mảng lớn) bên trong hàm cũng có thể chiếm dụng nhiều không gian trên Stack Frame, góp phần gây tràn stack nhanh hơn, đặc biệt khi hàm đó được gọi đệ quy.
4. Cài đặt Stack bằng mảng cố định bị đầy: Nếu bạn tự cài đặt cấu trúc dữ liệu Stack bằng mảng có kích thước cố định và liên tục thực hiện thao tác Push vượt quá kích thước đó mà không kiểm tra isFull.

Cách phòng tránh (ví dụ: khử đệ quy)

• Đảm bảo có Base Case: Luôn chắc chắn rằng hàm đệ quy của bạn có một hoặc nhiều trường hợp cơ sở rõ ràng để dừng việc tự gọi lại. Kiểm tra logic cẩn thận.
• Khử đệ quy (Tail Recursion Optimization / Iteration): Chuyển đổi thuật toán đệ quy thành dạng vòng lặp (iterative). Điều này loại bỏ việc sử dụng Call Stack để quản lý các lời gọi hàm lồng nhau. Một số trình biên dịch có thể tối ưu hóa đệ quy đuôi (tail recursion), nhưng không phải lúc nào cũng vậy. Sử dụng vòng lặp và có thể là một stack dữ liệu tường minh (explicit stack) thường an toàn hơn.
• Giới hạn độ sâu đệ quy: Nếu có thể, đặt ra giới hạn cho số lần gọi đệ quy.
• Tránh biến cục bộ lớn trên Stack: Nếu cần lưu trữ dữ liệu lớn, hãy cân nhắc cấp phát bộ nhớ trên Heap (ví dụ: sử dụng con trỏ, cấp phát động) thay vì khai báo biến cục bộ lớn trực tiếp trên Stack.
• Kiểm tra khi cài đặt Stack: Nếu tự cài đặt Stack bằng mảng, luôn kiểm tra isFull trước khi Push. Cân nhắc dùng cài đặt bằng danh sách liên kết nếu kích thước không xác định.

Tổng kết: Những điểm chính cần nhớ về Stack

Qua bài viết chi tiết này, hy vọng bạn đã có cái nhìn toàn diện và sâu sắc về cấu trúc dữ liệu Stack (ngăn xếp). Đây là những điểm cốt lõi cần ghi nhớ:

• Stack là gì? Là cấu trúc dữ liệu tuyến tính hoạt động theo nguyên tắc LIFO (Last-In, First-Out) – vào sau, ra trước.
• Thao tác chính: Push (thêm vào đỉnh), Pop (lấy ra khỏi đỉnh), Peek (xem đỉnh).
• Cách cài đặt: Có thể dùng Mảng (đơn giản, nhanh, kích thước cố định) hoặc Danh sách liên kết (linh hoạt, kích thước động).
• Ứng dụng: Rất đa dạng, từ quản lý lời gọi hàm/đệ quy, Undo/Redo, kiểm tra ngoặc, DFS, đến đánh giá biểu thức.
• Khác biệt với Queue: Stack là LIFO, Queue là FIFO (First-In, First-Out).
• Lỗi cần tránh: Stack Overflow, thường do đệ quy quá sâu hoặc vô hạn.

Stack, dù đơn giản, là một công cụ cực kỳ mạnh mẽ trong bộ công cụ của mọi lập trình viên. Nắm vững khái niệm và cách sử dụng Stack không chỉ giúp giải quyết nhiều bài toán hiệu quả mà còn là nền tảng để hiểu sâu hơn về cách máy tính hoạt động và quản lý bộ nhớ.