Stochastic Gradient Descent (SGD) là một thuật toán tối ưu mạnh mẽ và phổ biến trong học máy, đặc biệt đối với các bài toán có bộ dữ liệu lớn và phức tạp. Khác với phương pháp gradient descent truyền thống, SGD giúp tối ưu hóa các mô hình học máy bằng cách sử dụng một điểm dữ liệu ngẫu nhiên để cập nhật tham số, giúp tăng tốc độ hội tụ và hiệu quả tính toán.
Trong bài viết dưới đây, InterData sẽ cung cấp cái nhìn toàn diện về SGD là gì, cách thức hoạt động, những lợi ích và thách thức khi sử dụng thuật toán Stochastic Gradient Descent, cũng như các ứng dụng thực tế của thuật toán này trong các lĩnh vực. Đọc ngay nhé!
SGD là gì?
Stochastic Gradient Descent (SGD) là một kỹ thuật tối ưu hóa được sử dụng trong học máy để giảm thiểu lỗi trong các mô hình dự đoán. Khác với gradient descent thông thường, thuật toán này chỉ sử dụng một điểm dữ liệu tại mỗi lần tính toán gradient và cập nhật tham số mô hình.
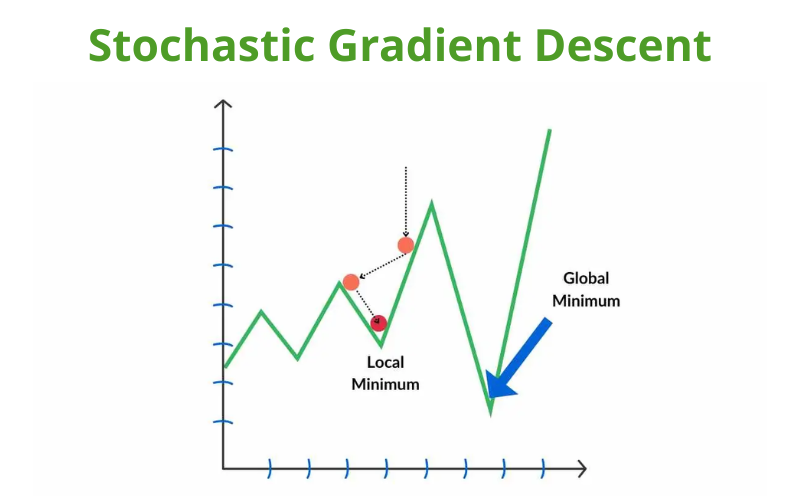
Thông qua việc này, SGD có thể nhanh chóng và hiệu quả hơn khi làm việc với các bộ dữ liệu lớn, mặc dù có thể gây ra sự nhiễu loạn và không ổn định. SGD giúp tìm ra giá trị tối ưu cho các tham số mô hình, từ đó cải thiện độ chính xác của dự đoán.
Cách thức hoạt động của SGD
Thuật toán Stochastic Gradient Descent hoạt động bằng cách cập nhật tham số của mô hình theo từng vòng lặp để giảm thiểu hàm mất mát đã xác định. Thuật toán bắt đầu với một tập tham số ban đầu, sau đó chọn ngẫu nhiên một lô hoặc một điểm dữ liệu từ bộ huấn luyện. Nó tính toán gradient của hàm mất mát liên quan đến dữ liệu đã chọn và điều chỉnh tham số theo hướng ngược lại với gradient.
Quá trình này được lặp lại qua nhiều lần cho đến khi mô hình hội tụ hoặc đạt tiêu chí dừng đã định.
Những lợi ích và thách thức của thuật toán SGD
Lợi ích của SGD là gì?
Stochastic Gradient Descent (SGD) là một thuật toán tối ưu mạnh mẽ trong học máy, mang lại nhiều ưu điểm nổi bật so với các thuật toán tối ưu khác. Những ưu điểm này khiến SGD trở thành lựa chọn phổ biến trong việc huấn luyện các mô hình, đặc biệt trong các tình huống có bộ dữ liệu lớn và các vấn đề tối ưu hóa phức tạp.
Hiệu quả với bộ dữ liệu lớn
Một trong những ưu điểm chính của SGD là hiệu quả khi xử lý bộ dữ liệu lớn. Bằng cách tính toán gradient với các mini-batch được chọn ngẫu nhiên, SGD có thể xử lý dữ liệu theo từng phần nhỏ, giảm yêu cầu bộ nhớ và gánh nặng tính toán. Điều này giúp SGD mở rộng hiệu quả đối với các bộ dữ liệu khổng lồ, thích hợp cho việc huấn luyện các mô hình trên các nền tảng big data.
Hội tụ nhanh hơn
SGD cập nhật tham số mô hình thường xuyên hơn so với batch gradient descent, dẫn đến hội tụ nhanh hơn. Tính ngẫu nhiên của SGD giúp quá trình tối ưu hóa trở nên linh động hơn, cho phép nó khám phá không gian giải pháp năng động và có thể hội tụ đến các giải pháp tốt hơn trong ít vòng lặp hơn.
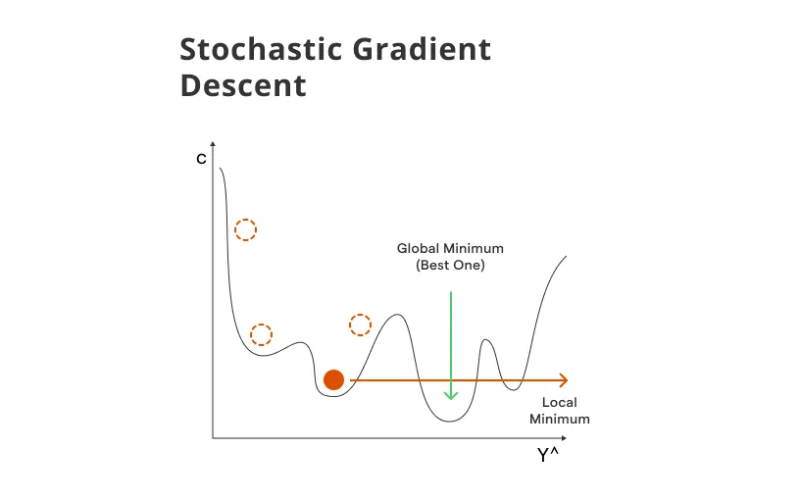
Thoát khỏi cực tiểu cục bộ
Tính ngẫu nhiên của thuật toán SGD đóng vai trò quan trọng trong việc giúp thuật toán thoát khỏi các cực tiểu cục bộ. Bằng cách đưa nhiễu vào quá trình tối ưu hóa thông qua việc lấy mẫu mini-batch ngẫu nhiên, SGD có thể điều hướng không gian tối ưu hóa hiệu quả hơn, tránh bị mắc kẹt ở các giải pháp không tối ưu.
Hiệu quả tính toán
So với batch gradient descent, yêu cầu tính toán gradient trên toàn bộ bộ dữ liệu, phương pháp mini-batch của SGD giúp giảm tải tính toán. SGD cập nhật tham số dựa trên gradient tính từ một phần của dữ liệu, giúp tăng tốc các vòng lặp và giảm chi phí tính toán.
Tính linh hoạt và khả năng thích ứng
SGD cung cấp tính linh hoạt trong việc điều chỉnh các siêu tham số, chẳng hạn như tỷ lệ học và kích thước mini-batch. Chúng ta có thể điều chỉnh các siêu tham số này để tối ưu hóa hiệu suất dựa trên đặc điểm của bộ dữ liệu và mô hình huấn luyện. Thêm vào đó, khả năng thích ứng của SGD giúp nó xử lý hiệu quả các phân phối dữ liệu không tĩnh và các tình huống học trực tuyến.
Cơ hội song song hóa
Phương pháp mini-batch của SGD rất thích hợp cho việc song song hóa, vì các phép tính cho các mini-batch khác nhau có thể được thực hiện đồng thời. Khả năng song song hóa này giúp tối ưu hóa việc sử dụng tài nguyên tính toán, đặc biệt trong các môi trường tính toán phân tán và các thiết lập tăng tốc GPU.
Ứng dụng trong nhiều mô hình khác nhau
Ưu điểm của SGD không chỉ áp dụng cho các mô hình học máy cụ thể. Nó có thể áp dụng cho nhiều nhiệm vụ học có giám sát và không giám sát khác nhau, bao gồm hồi quy tuyến tính, hồi quy logistic, mạng nơ-ron và các kiến trúc học sâu.
Hiểu được các ưu điểm của SGD là gì sẽ giúp nhấn mạnh hiệu quả và tính linh hoạt của nó như một thuật toán tối ưu trong học máy.
Thách thức của SGD là gì?
Stochastic Gradient Descent (SGD) là một thuật toán tối ưu mạnh mẽ, tuy nhiên nó cũng gặp phải một số thách thức có thể ảnh hưởng đến hiệu quả và sự hội tụ của nó. Việc hiểu rõ những thách thức này và áp dụng các giải pháp phù hợp là điều cần thiết để tối đa hóa hiệu suất của SGD trong quá trình huấn luyện mô hình học máy.
Gradient nhiễu
Tính ngẫu nhiên của SGD gây ra nhiễu trong việc ước tính gradient, dẫn đến sự dao động trong các cập nhật tham số và có thể cản trở quá trình hội tụ.
Giải pháp: Các kỹ thuật như trung bình gradient hoặc momentum có thể giúp giảm thiểu tác động của gradient nhiễu. Trung bình gradient bao gồm việc tích lũy gradient qua nhiều vòng lặp để làm mượt các dao động, trong khi momentum thêm một yếu tố vận tốc vào các cập nhật tham số để ổn định quá trình.
Vấn đề hội tụ
SGD có thể thể hiện hành vi hội tụ không ổn định, dao động quanh giải pháp tối ưu hoặc hội tụ đến các điểm tối ưu kém.
Giải pháp: Sử dụng các lịch trình tỷ lệ học thích ứng hoặc kỹ thuật làm nguội có thể giúp tăng cường sự ổn định của quá trình hội tụ. Các kỹ thuật như giảm tỷ lệ học giúp giảm dần tỷ lệ học theo thời gian, cho phép SGD điều chỉnh các cập nhật tham số khi gần đến giải pháp tối ưu.
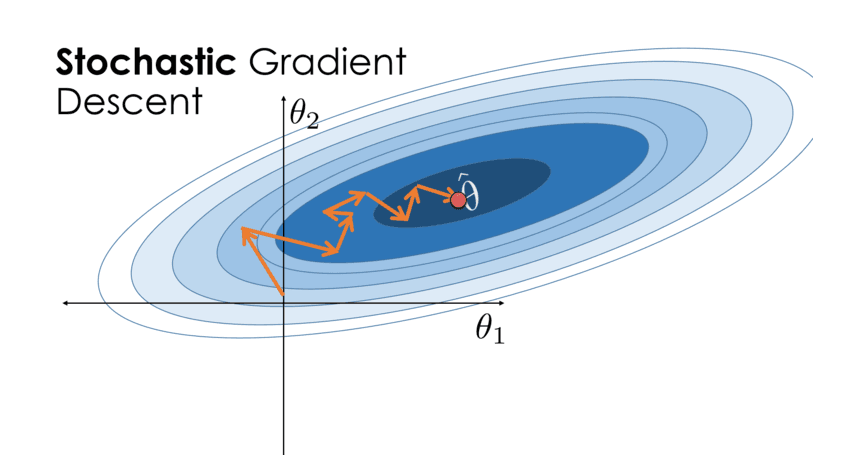
Độ nhạy với tỷ lệ học
Việc chọn tỷ lệ học phù hợp trong SGD có thể ảnh hưởng lớn đến hiệu suất tối ưu hóa. Tỷ lệ học quá cao có thể khiến thuật toán không hội tụ, trong khi tỷ lệ học quá thấp có thể làm chậm quá trình hội tụ.
Giải pháp: Sử dụng các lịch trình tỷ lệ học, phương pháp tỷ lệ học thích ứng, hoặc kỹ thuật như làm ấm tỷ lệ học có thể giải quyết vấn đề nhạy cảm với tỷ lệ học. Các phương pháp thích ứng điều chỉnh động tỷ lệ học dựa trên lịch sử cập nhật tham số. Ngược lại, làm ấm tỷ lệ học tăng dần tỷ lệ học vào đầu quá trình huấn luyện để đẩy nhanh quá trình hội tụ.
Hiện tượng overfitting (quá khớp)
SGD dễ bị overfitting, đặc biệt khi huấn luyện các mô hình phức tạp có khả năng ghi nhớ nhiễu trong dữ liệu huấn luyện.
Giải pháp: Các kỹ thuật regularization như L1 hoặc L2 regularization, dropout hoặc dừng sớm có thể giúp chống lại overfitting. Các phương pháp regularization phạt các mô hình quá phức tạp hoặc thêm nhiễu trong quá trình huấn luyện để tránh việc quá phụ thuộc vào các điểm dữ liệu đơn lẻ.
Tối ưu hóa siêu tham số
Việc lựa chọn các siêu tham số phù hợp, như tỷ lệ học, kích thước mini-batch và mức độ regularization, có thể là một thách thức và mất nhiều thời gian.
Giải pháp: Sử dụng các kỹ thuật tối ưu hóa siêu tham số như tìm kiếm lưới (grid search), tìm kiếm ngẫu nhiên (random search) hoặc tối ưu hóa Bayes có thể tự động hóa quá trình tối ưu hóa siêu tham số, giúp tìm các cấu hình tối ưu nhanh chóng.
Tài nguyên tính toán
Việc huấn luyện mô hình với SGD có thể yêu cầu tài nguyên tính toán đáng kể, đặc biệt đối với các bộ dữ liệu lớn và mô hình phức tạp.
Giải pháp: Sử dụng các framework tính toán phân tán và kỹ thuật song song, hoặc sử dụng các bộ tăng tốc phần cứng như GPU hoặc TPU có thể tăng tốc quá trình huấn luyện và cải thiện khả năng mở rộng.
Giải quyết những thách thức này với các giải pháp phù hợp giúp các nhà thực hành khai thác tối đa tiềm năng của Stochastic Gradient Descent trong việc huấn luyện các mô hình học máy.
Bằng cách giảm thiểu các vấn đề như gradient nhiễu, sự không ổn định trong hội tụ và overfitting, SGD có thể tối ưu hóa hiệu quả các mô hình, mang lại hiệu suất và khả năng tổng quát tốt hơn trong các lĩnh vực khác nhau.
Các biến thể của Stochastic Gradient Descent
Dù SGD truyền thống là một phương pháp mạnh mẽ, nhưng có một số cải tiến và biến thể được thiết kế để cải thiện sự hội tụ và tính ổn định:
Stochastic Gradient Descent (SGD) là nền tảng của nhiều thuật toán tối ưu, mỗi biến thể đều có các cải tiến và điều chỉnh riêng để giải quyết các thách thức đặc thù trong quá trình huấn luyện mô hình.
Việc hiểu rõ các biến thể Stochastic Gradient Descent là gì là rất quan trọng để tùy chỉnh chiến lược tối ưu hóa cho các trường hợp sử dụng cụ thể, từ đó nâng cao hiệu quả và hiệu suất huấn luyện mô hình.
Mini-batch Stochastic Gradient Descent (Mini-batch SGD)
Mini-batch SGD tạo ra sự cân bằng giữa hiệu quả của SGD và tính ổn định của batch gradient descent bằng cách tính toán gradient sử dụng một tập con ngẫu nhiên (mini-batch) của dữ liệu huấn luyện.
Mini-batch SGD mang lại tốc độ hội tụ nhanh hơn so với SGD thuần túy, tận dụng lợi ích của cả hai phương pháp SGD và batch gradient descent. Nó cho phép sử dụng tài nguyên tính toán hiệu quả và hỗ trợ việc song song hóa.
Momentum Stochastic Gradient Descent
Momentum SGD cải thiện SGD truyền thống bằng cách thêm một yếu tố động lượng vào các cập nhật tham số, giúp tăng tốc các cập nhật trong hướng của gradient bền vững và giảm dao động.
Giúp SGD vượt qua các thách thức liên quan đến gradient nhiễu và cải thiện sự ổn định của hội tụ bằng cách làm mượt các cập nhật tham số. Nó giúp tăng tốc quá trình tối ưu hóa trong các thung lũng nông và dài trong không gian tối ưu hóa.
Nesterov Accelerated Gradient (NAG)
Nesterov Accelerated Gradient, hay Nesterov Momentum, điều chỉnh Momentum SGD bằng cách đánh giá gradient ở vị trí đã điều chỉnh, dự đoán và sửa chữa sự vượt quá do động lượng gây ra.
NAG cải thiện tốc độ và độ chính xác của hội tụ bằng cách xem xét sự vượt quá do động lượng gây ra, giúp tối ưu hóa mượt mà hơn và hội tụ nhanh chóng đến giải pháp tối ưu.
AdaGrad (Adaptive Gradient Algorithm)
AdaGrad điều chỉnh tỷ lệ học cho mỗi tham số dựa trên gradient lịch sử, giảm tỷ lệ học cho các tham số được cập nhật thường xuyên và tăng tỷ lệ học cho các tham số ít được cập nhật.
AdaGrad xử lý hiệu quả dữ liệu thưa thớt và các tỷ lệ đặc tính không đồng đều bằng cách tự động điều chỉnh tỷ lệ học. Nó thúc đẩy hội tụ nhanh hơn và cải thiện tính ổn định, đặc biệt trong các trường hợp có gradient thay đổi.
RMSProp (Root Mean Square Propagation)
RMSProp giải quyết vấn đề tỷ lệ học giảm dần trong AdaGrad bằng cách giới thiệu một trung bình suy giảm theo cấp số mũ của gradient bình phương, điều chỉnh tỷ lệ học bằng căn bậc hai của gradient gần đây.
RMSProp giảm thiểu nguy cơ giảm tỷ lệ học quá mạnh trong AdaGrad, giúp tối ưu hóa ổn định và thích ứng hơn. Nó đặc biệt hiệu quả trong các tác vụ học sâu với gradient không ổn định hoặc thưa thớt.
Adam (Adaptive Moment Estimation)
Adam kết hợp các lợi ích của Momentum SGD và RMSProp bằng cách duy trì cả yếu tố động lượng và một trung bình suy giảm theo cấp số mũ của gradient quá khứ, điều chỉnh tỷ lệ học cho mỗi tham số.
Adam cung cấp sự hội tụ nhanh chóng, khả năng chống lại các siêu tham số và xử lý hiệu quả gradient nhiễu. Nó được sử dụng rộng rãi trong học sâu và huấn luyện mạng nơ-ron nhờ vào khả năng điều chỉnh tỷ lệ học và hiệu quả tính toán.
Hiểu được sự khác biệt giữa các biến thể của thuật toán SGD giúp các nhà thực hành chọn lựa và điều chỉnh thuật toán tối ưu cho các tác vụ và bộ dữ liệu học máy cụ thể. Bằng cách tận dụng điểm mạnh của mỗi biến thể, các nhà thực hành có thể tăng tốc độ hội tụ, tính ổn định và hiệu suất mô hình, cuối cùng đạt được kết quả vượt trội trong các lĩnh vực đa dạng.
Sự khác biệt giữa SGD và Batch Gradient Descent
Batch Gradient Descent (BGD) và Stochastic Gradient Descent (SGD) là hai biến thể của thuật toán gradient descent được sử dụng để huấn luyện các mô hình học máy.
Mặc dù chúng cùng chia sẻ nguyên lý cơ bản là cập nhật tham số mô hình qua các vòng lặp để giảm thiểu hàm mất mát, nhưng chúng khác biệt rõ rệt trong cách tính toán gradient và cập nhật tham số.
Tính toán gradient:
-
- BGD: Tính toán gradient của hàm mất mát đối với tất cả các ví dụ huấn luyện trong bộ dữ liệu.
- SGD: Tính toán gradient của hàm mất mát chỉ với một ví dụ huấn luyện ngẫu nhiên (hoặc một mini-batch nhỏ).
Cập nhật tham số:
-
- BGD: Cập nhật tham số mô hình dựa trên gradient trung bình tính toán từ toàn bộ bộ dữ liệu.
- SGD: Cập nhật tham số mô hình dựa trên gradient tính toán từ một ví dụ huấn luyện (hoặc mini-batch).
Hành vi hội tụ:
-
- BGD: Thường hội tụ đến tối thiểu toàn cục của hàm mất mát đối với các bài toán lồi. Quá trình hội tụ mượt mà và ổn định hơn so với SGD.
- SGD: Quá trình hội tụ có thể dao động nhiều hơn do tính ngẫu nhiên của việc ước tính gradient. Tuy nhiên, nó thích hợp hơn cho các bài toán không lồi và có thể dễ dàng thoát khỏi các cực tiểu cục bộ.
Hiệu quả tính toán:
-
- BGD: Cần phải xử lý toàn bộ bộ dữ liệu trong mỗi vòng lặp, do đó có thể tốn kém về tính toán, đặc biệt là với các bộ dữ liệu lớn.
- SGD: Hiệu quả tính toán hơn, vì nó chỉ xử lý một ví dụ huấn luyện (hoặc mini-batch) trong mỗi vòng lặp. Thích hợp cho các bộ dữ liệu lớn và các tình huống học trực tuyến.
Nhiễu trong ước tính gradient:
-
- BGD: Gradient tính toán từ toàn bộ bộ dữ liệu ít bị nhiễu, dẫn đến các quỹ đạo tối ưu hóa mượt mà hơn.
- SGD: Gradient tính toán từ một ví dụ huấn luyện (hoặc mini-batch) có thể bị nhiễu, tạo ra sự ngẫu nhiên trong quá trình tối ưu hóa. Điều này giúp SGD thoát khỏi các cực tiểu cục bộ và khám phá không gian giải pháp hiệu quả hơn.
BGD và SGD khác nhau về cách tính toán gradient, cập nhật tham số, hành vi hội tụ, hiệu quả tính toán và nhiễu trong ước tính gradient. BGD phù hợp với các bộ dữ liệu nhỏ và bài toán với hàm mất mát lồi, trong khi SGD hiệu quả hơn cho các bộ dữ liệu lớn và bài toán không lồi, mang lại sự hội tụ nhanh hơn và khả năng mở rộng tốt hơn.
Ứng dụng của SGD – Stochastic Gradient Descent
Thuật toán Stochastic Gradient Descent và các biến thể của nó đóng vai trò quan trọng trong nhiều nhiệm vụ học máy, từ các mô hình tuyến tính truyền thống đến các mạng nơ-ron sâu phức tạp. Hiệu quả, khả năng mở rộng và tính thích ứng của SGD khiến nó không thể thiếu trong nhiều ứng dụng trên các lĩnh vực đa dạng.
Huấn luyện mạng Nơ-ron Sâu:
SGD và các biến thể của nó, đặc biệt là Adam và RMSProp, được sử dụng rộng rãi trong huấn luyện các mạng nơ-ron sâu (DNNs). Các thuật toán tối ưu này giúp huấn luyện hiệu quả các DNNs với hàng triệu tham số, thúc đẩy các bước đột phá trong nhận diện hình ảnh, xử lý ngôn ngữ tự nhiên và học củng cố.
Hồi quy tuyến tính và hồi quy Logistic:
SGD là kỹ thuật tối ưu cơ bản để huấn luyện các mô hình hồi quy tuyến tính và hồi quy logistic. Khả năng xử lý các bộ dữ liệu lớn và hội tụ nhanh giúp SGD phù hợp với các nhiệm vụ hồi quy trong tài chính, y tế và marketing.
Máy hỗ trợ Vectơ (SVM):
Các thuật toán tối ưu dựa trên SGD thường được sử dụng trong huấn luyện máy hỗ trợ vectơ (SVM) cho các nhiệm vụ phân loại. SVM với tối ưu hóa SGD được sử dụng rộng rãi trong phân loại văn bản, phân loại hình ảnh và ứng dụng sinh học.
Hệ thống đề xuất:
Thuật toán SGD đóng vai trò quan trọng trong việc huấn luyện các mô hình lọc cộng tác cho hệ thống đề xuất. Những mô hình này sử dụng SGD để học sở thích người dùng và đưa ra các gợi ý cá nhân hóa trong các nền tảng thương mại điện tử, phát trực tuyến và mạng xã hội.

Xử lý ngôn ngữ tự nhiên (NLP):
SGD và các biến thể của nó là phần không thể thiếu trong huấn luyện các mô hình học máy cho các nhiệm vụ NLP, bao gồm phân tích cảm xúc, nhận diện thực thể có tên và dịch máy. Các mô hình như mạng nơ-ron hồi quy (RNNs) và transformers sử dụng tối ưu hóa dựa trên SGD để học các mẫu phức tạp trong dữ liệu văn bản.
Nhận diện hình ảnh và bật thể:
Thuật toán tối ưu hóa SGD rất quan trọng trong việc huấn luyện các mạng nơ-ron tích chập (CNNs) cho các nhiệm vụ phân loại hình ảnh, phát hiện vật thể và phân đoạn. Các CNNs được huấn luyện bằng SGD được sử dụng trong xe tự lái, hệ thống giám sát và phân tích hình ảnh y tế.
Học củng cố:
Trong học củng cố (RL), SGD và các biến thể của nó tối ưu hóa các bộ xấp xỉ chính sách và hàm giá trị. Tối ưu hóa dựa trên SGD cho phép các tác nhân học các chiến lược tối ưu trong môi trường phức tạp, dẫn đến các bước tiến trong robot, trò chơi và hệ thống tự động.
Học trực tuyến:
Khả năng thích ứng của SGD với dữ liệu streaming và môi trường không tĩnh khiến nó rất phù hợp cho các tình huống học trực tuyến. Các ứng dụng học trực tuyến bao gồm phát hiện bất thường theo thời gian thực, đề xuất nội dung cá nhân hóa và hệ thống điều khiển thích ứng.
Mạng đối kháng tạo sinh (GANs):
Thuật toán tối ưu hóa SGD huấn luyện các mạng đối kháng sinh tạo (GANs) để tạo ra hình ảnh, video và âm thanh thực tế. GANs được huấn luyện bằng SGD được sử dụng trong tạo nghệ thuật, chỉnh sửa hình ảnh và tăng cường dữ liệu.
Từ việc huấn luyện các mô hình học sâu tiên tiến đến tối ưu hóa các thuật toán học máy truyền thống, SGD và các biến thể của nó tìm thấy nhiều ứng dụng rộng rãi trong nhiều lĩnh vực. Tính linh hoạt, hiệu quả và hiệu suất của chúng khiến chúng trở thành công cụ không thể thiếu để giải quyết các thách thức học máy và thúc đẩy sự đổi mới trong trí tuệ nhân tạo.
Khi triển khai các mô hình học máy như Stochastic Gradient Descent (SGD), việc lựa chọn một hạ tầng mạnh mẽ là rất quan trọng. Tại InterData, dịch vụ thuê VPS chất lượng uy tín của chúng tôi cung cấp phần cứng thế hệ mới với CPU AMD EPYC/Intel Xeon Platinum và SSD NVMe U.2, giúp bạn xử lý dữ liệu nhanh chóng và ổn định.
Ngoài ra, nếu bạn cần hiệu suất cao hơn, thuê Cloud Server giá rẻ tại InterData là lựa chọn lý tưởng. Với dung lượng được tối ưu và băng thông cao, các máy chủ đám mây này giúp bạn huấn luyện mô hình học máy hiệu quả, tiết kiệm chi phí mà vẫn đảm bảo chất lượng và tốc độ xử lý.
Liên hệ InterData ngay để được tư vấn chi tiết!
INTERDATA
- Website: Interdata.vn
- Hotline: 1900-636822
- Email: [email protected]
- VPĐD: 240 Nguyễn Đình Chính, P.11. Q. Phú Nhuận, TP. Hồ Chí Minh
- VPGD: Số 211 Đường số 5, KĐT Lakeview City, P. An Phú, TP. Thủ Đức, TP. Hồ Chí Minh








![Hướng dẫn cài đặt n8n trên VPS Ubuntu InterData [2025] 12 Cài đặt n8n trên VPS Ubuntu](https://interdata.vn/blog/wp-content/uploads/2025/05/Cai-dat-n8n-tren-VPS-Ubuntu-120x86.jpg)

