PCA là gì? Thông tin nên biết về Principal Component Analysis

Principal Component Analysis (PCA) là một kỹ thuật giảm chiều dữ liệu mạnh mẽ và phổ biến trong khoa học dữ liệu, giúp đơn giản hóa các tập dữ liệu phức tạp mà vẫn giữ được phần lớn thông tin cốt lõi. Bài viết này sẽ giúp bạn hiểu rõ PCA là gì, cách hoạt động, cùng với ưu – nhược điểm và các ứng dụng thực tế để bạn có thể hiểu chi tiết hơn về phân tích thành phần chính – PCA.

PCA là gì?

Principal Component Analysis – PCA (Phân tích thành phần chính) được biết đến là một phương pháp thông dụng để thu gọn số chiều của dữ liệu trong ngành khoa học dữ liệu. Trọng tâm của PCA là làm giảm đi số lượng thuộc tính (biến) của một bộ dữ liệu, nhưng đồng thời phải cố gắng bảo toàn tối đa lượng thông tin cốt lõi chứa đựng trong đó.

Người ta ứng dụng PCA nhằm xử lý những thách thức nảy sinh từ sự phức tạp của dữ liệu, qua đó góp phần nâng cao hiệu quả hoạt động của các mô hình học máy.

Lý do nên dùng PCA?

Việc xử lý các bộ dữ liệu có quy mô lớn thường gặp trở ngại do số lượng đặc trưng (biến) quá nhiều, khiến cho việc minh họa dữ liệu bằng hình ảnh và tiến hành phân tích trở nên phức tạp. PCA mang lại giải pháp thông qua các lợi ích sau:

• Thu gọn không gian đặc trưng: Kỹ thuật này giúp đơn giản hóa cấu trúc dữ liệu, làm cho mô hình bớt phức tạp hơn.
• Loại bỏ thông tin nhiễu: PCA ưu tiên các thành phần chứa nhiều thông tin nhất (thành phần chính), nhờ đó có thể loại bỏ những đặc trưng ít đóng góp hoặc gây nhiễu.
• Tăng cường hiệu quả mô hình: Việc giảm chiều dữ liệu giúp rút ngắn thời gian cần thiết cho quá trình huấn luyện mô hình cũng như khi mô hình thực hiện dự đoán.

Cách thức hoạt động của PCA

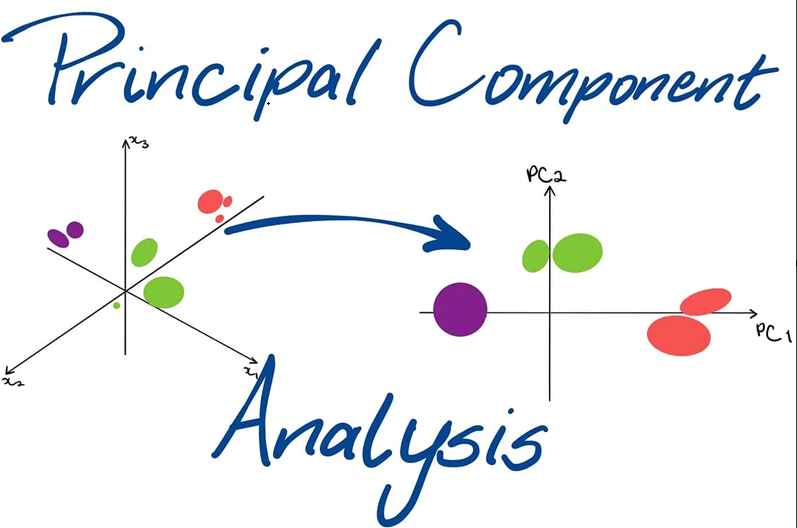
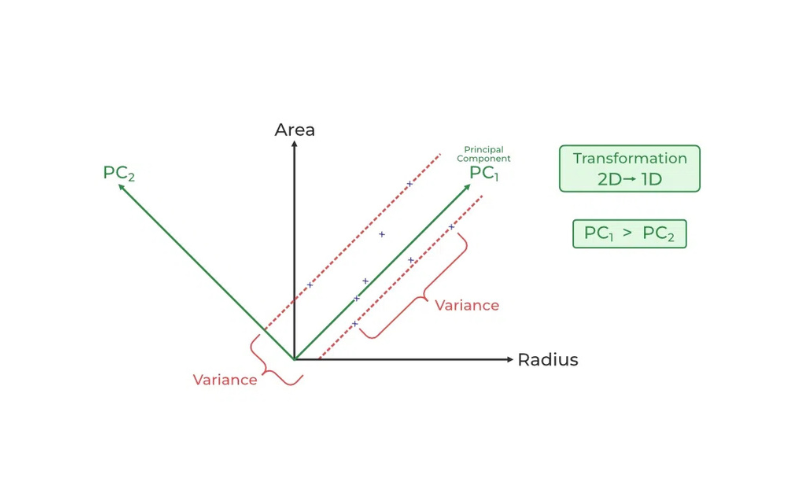
PCA tóm tắt nội dung thông tin của các bộ dữ liệu lớn vào một tập hợp nhỏ các biến không tương quan, được gọi là các thành phần chính. Các thành phần chính này là các tổ hợp tuyến tính của các biến gốc, có phương sai lớn nhất so với các tổ hợp tuyến tính khác. Các thành phần này sẽ nắm bắt càng nhiều thông tin từ bộ dữ liệu gốc càng tốt.

Kỹ thuật thống kê này bao gồm cả đại số tuyến tính và các phép toán ma trận, và nó biến đổi bộ dữ liệu gốc thành một hệ tọa độ mới được cấu trúc bởi các thành phần chính. Các vectơ riêng và giá trị riêng từ ma trận hiệp phương sai, là cơ sở của các thành phần chính, cho phép phân tích các phép biến đổi tuyến tính này.

Hãy tưởng tượng bạn có một bộ dữ liệu với nhiều đặc trưng, kết quả là một biểu đồ phân tán đa chiều. Các vectơ riêng cung cấp hướng biến thiên trong biểu đồ phân tán. Giá trị riêng là các hệ số của các vectơ riêng, cho biết mức độ quan trọng của dữ liệu theo hướng đó.

Do đó, giá trị riêng cao có nghĩa là vectơ riêng tương ứng quan trọng hơn. Vì các thành phần chính đại diện cho các hướng có phương sai tối đa trong dữ liệu, chúng cũng chính là các vectơ riêng của ma trận hiệp phương sai.

Hai thành phần chính chính được tính trong PCA: thành phần chính đầu tiên (PC1) và thành phần chính thứ hai (PC2).

Ưu và Nhược điểm của Principal Component Analysis – PCA

Ưu điểm của PCA

• Xử lý đa cộng tuyến: PCA tạo ra các biến mới không có mối tương quan để giải quyết vấn đề khi các đặc trưng gốc có sự tương quan cao.
• Giảm nhiễu: PCA loại bỏ các thành phần có phương sai thấp (được cho là nhiễu), giúp làm rõ dữ liệu.
• Nén dữ liệu: Đại diện dữ liệu với ít thành phần hơn, giảm nhu cầu lưu trữ và tăng tốc độ xử lý.
• Phát hiện điểm ngoại lai: PCA xác định các điểm dữ liệu bất thường bằng cách chỉ ra những điểm lệch lạc đáng kể trong không gian giảm chiều.

Nhược điểm của PCA

• Khó khăn trong việc giải thích: Các thành phần mới là sự kết hợp của các biến gốc, điều này có thể khó giải thích.
• Nhạy cảm với tỷ lệ dữ liệu: PCA yêu cầu dữ liệu được chuẩn hóa đúng cách trước khi áp dụng, nếu không kết quả có thể gây hiểu lầm.
• Mất thông tin: Việc giảm chiều có thể làm mất một số thông tin quan trọng nếu giữ quá ít thành phần.
• Giả định tuyến tính: PCA hoạt động tốt nhất khi mối quan hệ giữa các biến là tuyến tính và có thể gặp khó khăn với dữ liệu phi tuyến tính.
• Độ phức tạp tính toán: PCA có thể chậm và tiêu tốn tài nguyên khi xử lý dữ liệu rất lớn.
• Nguy cơ overfitting: Việc sử dụng quá nhiều thành phần hoặc làm việc với một bộ dữ liệu nhỏ có thể dẫn đến các mô hình không có khả năng tổng quát tốt.

PCA giúp cô đọng dữ liệu phức tạp thành các yếu tố thông tin quan trọng nhất, làm cho quá trình phân tích trở nên đơn giản và hiệu quả hơn.

PCA xác định các phương hướng (gọi là thành phần chính) nơi dữ liệu thay đổi nhiều nhất. Sau đó, PCA chiếu dữ liệu lên những phương hướng này, giảm số chiều của dữ liệu nhưng vẫn giữ lại càng nhiều thông tin càng tốt. Tập hợp các biến không tương quan mới (thành phần chính) sẽ dễ làm việc hơn và có thể được sử dụng cho các nhiệm vụ như hồi quy, phân loại hoặc trực quan hóa.

So sánh PCA với K-means clustering

PCA và K-means clustering đều là các kỹ thuật học máy không giám sát được sử dụng trong phân tích dữ liệu, nhưng chúng có mục tiêu và phương pháp khác nhau. PCA được sử dụng để giảm chiều dữ liệu, trong khi K-means clustering nhóm các điểm dữ liệu lại với nhau dựa trên sự tương đồng. Kỹ thuật bạn chọn phụ thuộc vào bộ dữ liệu cụ thể và mục tiêu phân tích của bạn.

PCA tạo ra các biến mới, như các thành phần chính, là các tổ hợp tuyến tính của các biến gốc. PCA nhận đầu vào là một bộ dữ liệu với nhiều biến và tạo ra một bộ dữ liệu trong không gian con thấp hơn, tức là một bộ dữ liệu được giảm chiều với ít biến hơn. Nó thường được sử dụng trong phân tích dữ liệu khám phá để xây dựng các mô hình dự đoán, nhưng cũng được dùng trong tiền xử lý dữ liệu để giảm chiều.

K-means là một thuật toán phân cụm, gán các điểm dữ liệu vào các nhóm dựa trên khoảng cách từ các tâm cụm. Nó nhận đầu vào là một bộ dữ liệu với một hoặc nhiều biến và tạo ra một tập hợp các nhóm với các điểm dữ liệu tương tự nhau. Nó thường được sử dụng để phân cụm dữ liệu cho nhiều mục đích khác nhau, như phân đoạn hình ảnh, phân nhóm khách hàng và phát hiện bất thường.

Ứng dụng của Principal Component Analysis

Áp dụng PCA có thể giúp tiền xử lý hoặc trích xuất các đặc trưng thông tin quan trọng nhất từ các bộ dữ liệu có nhiều biến. Tiền xử lý giúp giảm độ phức tạp trong khi vẫn giữ lại thông tin quan trọng.

Một số ứng dụng phổ biến của PCA bao gồm:

• Nén hình ảnh: PCA giảm chiều của hình ảnh trong khi vẫn giữ lại các thông tin thiết yếu. Nó giúp tạo ra các đại diện hình ảnh gọn nhẹ hơn, làm cho việc lưu trữ và truyền tải hình ảnh dễ dàng hơn.
• Trực quan hóa dữ liệu: PCA giúp trực quan hóa dữ liệu có nhiều chiều bằng cách chiếu nó vào không gian có ít chiều hơn, chẳng hạn như biểu đồ 2D hoặc 3D. Điều này làm cho việc giải thích và khám phá dữ liệu trở nên đơn giản hơn.
• Lọc nhiễu: PCA có thể loại bỏ nhiễu hoặc thông tin dư thừa khỏi dữ liệu bằng cách tập trung vào các thành phần chính nắm bắt các mô hình cơ bản.
• Dự đoán ung thư vú: PCA cũng đã được ứng dụng trong y tế. Ví dụ, nó đã hỗ trợ trong việc chẩn đoán bệnh sớm và chính xác hơn. Bài báo “Breast Cancer Prediction using Principal Component Analysis with Logistic Regression” phân tích bộ dữ liệu ung thư vú nổi tiếng được thu thập từ bệnh nhân tại Bệnh viện Đại học Wisconsin, Madison.

Một thuật toán phân loại học giám sát, hồi quy logistic, được áp dụng để dự đoán liệu bệnh ung thư vú có xuất hiện hay không.

Khi nào nên sử dụng Principal Component Analysis

Có nhiều kỹ thuật giảm chiều khác có sẵn, bao gồm phân tích phân biệt tuyến tính (LDA), rừng ngẫu nhiên (Random Forest), xấp xỉ và chiếu đa diện đồng nhất (UMAP), và láng giềng ngẫu nhiên t-distributed (t-SNE).

Hãy cân nhắc các yếu tố sau để quyết định liệu PCA có phải là phương pháp phù hợp cho phân tích của bạn không:

• Tính tuyến tính: PCA là một kỹ thuật tuyến tính, trong khi các kỹ thuật khác như t-SNE và UMAP lại phi tuyến. Điều này có nghĩa là PCA phù hợp hơn với các bộ dữ liệu có mối quan hệ tuyến tính giữa các biến. Các kỹ thuật phi tuyến phù hợp hơn với các bộ dữ liệu có mối quan hệ phi tuyến hoặc phức tạp hơn giữa các biến.
• Tính toán: PCA sử dụng các phép toán ma trận để tính toán và quản lý hiệu quả các bộ dữ liệu lớn. Các kỹ thuật khác như t-SNE và UMAP lại đắt đỏ và có thể không phù hợp với các bộ dữ liệu lớn.
• Bảo tồn thông tin: PCA bảo tồn tối đa phương sai trong dữ liệu. t-SNE và UMAP tập trung vào việc bảo tồn cấu trúc cục bộ của dữ liệu. Do đó, PCA phù hợp hơn trong việc xác định các biến quan trọng nhất trong dữ liệu. Các kỹ thuật phi tuyến phù hợp hơn để trực quan hóa dữ liệu trong không gian có ít chiều.
• Trích xuất đặc trưng: PCA là một kỹ thuật trích xuất đặc trưng. Nó tạo ra các biến mới là các tổ hợp tuyến tính của các biến gốc. Các kỹ thuật khác (như UMAP và t-SNE) không tạo ra các biến mới. Điều này có nghĩa là PCA có thể xác định các biến quan trọng nhất trong dữ liệu. Các kỹ thuật phi tuyến phù hợp hơn để trực quan hóa dữ liệu trong không gian có ít chiều.

Principal Component Analysis là một công cụ hữu ích để xử lý dữ liệu có nhiều đặc trưng, giúp nâng cao hiệu suất mô hình và khả năng trực quan hóa. Tuy nhiên, việc áp dụng PCA cũng cần cân nhắc kỹ lưỡng để đảm bảo không làm mất đi những thông tin quan trọng.

Khi xử lý các thuật toán như PCA trên tập dữ liệu lớn, việc lựa chọn hạ tầng máy chủ mạnh mẽ và ổn định là điều quan trọng. Tại InterData, bạn có thể thuê VPS chất lượng giá rẻ và thuê Cloud Server tốc độ cao, với phần cứng hiện đại như CPU AMD EPYC hoặc Intel Xeon Platinum, SSD NVMe U.2 tốc độ cao, băng thông lớn và dung lượng tối ưu cho nhu cầu học máy, phân tích dữ liệu hay chạy mô hình AI.